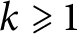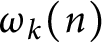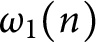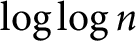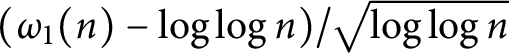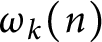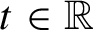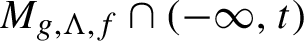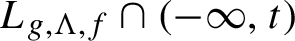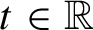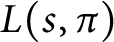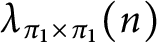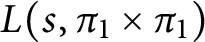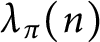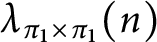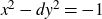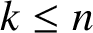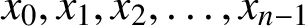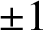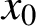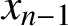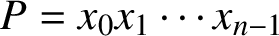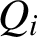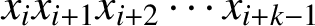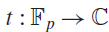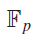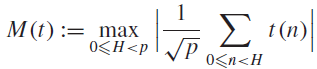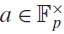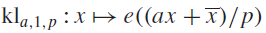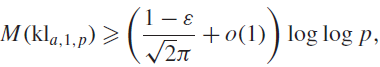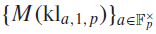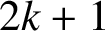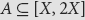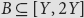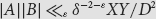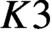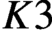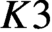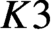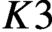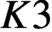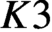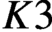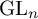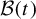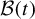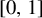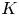Refine listing
Actions for selected content:
2812 results in 11xxx
Cyclicity of elliptic curves modulo primes in arithmetic progressions
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 74 / Issue 5 / October 2022
- Published online by Cambridge University Press:
- 03 May 2021, pp. 1277-1309
- Print publication:
- October 2022
-
- Article
- Export citation
Number of prime factors with a given multiplicity
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 65 / Issue 1 / March 2022
- Published online by Cambridge University Press:
- 03 May 2021, pp. 253-269
- Print publication:
- March 2022
-
- Article
- Export citation
Fourier transforms related to ζ(s)
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 64 / Issue 2 / May 2021
- Published online by Cambridge University Press:
- 30 April 2021, pp. 200-216
-
- Article
- Export citation
A note on extensions of multilinear maps defined on multilinear varieties
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 64 / Issue 2 / May 2021
- Published online by Cambridge University Press:
- 30 April 2021, pp. 148-173
-
- Article
- Export citation
Additive bases via Fourier analysis
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 30 / Issue 6 / November 2021
- Published online by Cambridge University Press:
- 29 April 2021, pp. 930-941
-
- Article
- Export citation
Singular units and isogenies between CM elliptic curves
- Part of
-
- Journal:
- Compositio Mathematica / Volume 157 / Issue 5 / May 2021
- Published online by Cambridge University Press:
- 29 April 2021, pp. 1022-1035
- Print publication:
- May 2021
-
- Article
- Export citation
Explicit methods for the Hasse norm principle and applications to An and Sn extensions
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 172 / Issue 3 / May 2022
- Published online by Cambridge University Press:
- 22 April 2021, pp. 489-529
- Print publication:
- May 2022
-
- Article
-
- You have access
- Open access
- Export citation
Continuity of Hausdorff dimension across generic dynamical Lagrange and Markov spectra II
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 42 / Issue 6 / June 2022
- Published online by Cambridge University Press:
- 22 April 2021, pp. 1898-1907
- Print publication:
- June 2022
-
- Article
- Export citation
Cancellation of two classes of dirichlet coefficients over Beatty sequences
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 65 / Issue 1 / March 2022
- Published online by Cambridge University Press:
- 20 April 2021, pp. 234-252
- Print publication:
- March 2022
-
- Article
- Export citation
Redei reciprocity, governing fields and negative Pell
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 172 / Issue 3 / May 2022
- Published online by Cambridge University Press:
- 19 April 2021, pp. 627-654
- Print publication:
- May 2022
-
- Article
-
- You have access
- Open access
- Export citation
ASKING QUESTIONS TO DETERMINE THE PRODUCT OF CIRCULARLY ARRANGED NUMBERS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 104 / Issue 2 / October 2021
- Published online by Cambridge University Press:
- 19 April 2021, pp. 187-195
- Print publication:
- October 2021
-
- Article
- Export citation
On the size of the maximum of incomplete Kloosterman sums
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 172 / Issue 3 / May 2022
- Published online by Cambridge University Press:
- 15 April 2021, pp. 563-590
- Print publication:
- May 2022
-
- Article
-
- You have access
- Open access
- Export citation
ON ASYMPTOTIC BASES WHICH HAVE DISTINCT SUBSET SUMS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 104 / Issue 2 / October 2021
- Published online by Cambridge University Press:
- 12 April 2021, pp. 211-217
- Print publication:
- October 2021
-
- Article
- Export citation
On the distribution of nonprimitive lattice points in the plane
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 65 / Issue 1 / March 2022
- Published online by Cambridge University Press:
- 08 April 2021, pp. 198-207
- Print publication:
- March 2022
-
- Article
- Export citation
Extremal problems for GCDs
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 30 / Issue 6 / November 2021
- Published online by Cambridge University Press:
- 08 April 2021, pp. 922-929
-
- Article
-
- You have access
- Open access
- Export citation
CM liftings of
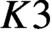 $K3$ surfaces over finite fields and their applications to the Tate conjecture
$K3$ surfaces over finite fields and their applications to the Tate conjecture
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 9 / 2021
- Published online by Cambridge University Press:
- 08 April 2021, e29
-
- Article
-
- You have access
- Open access
- Export citation
HECKE OPERATORS AND THE COHERENT COHOMOLOGY OF SHIMURA VARIETIES
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 22 / Issue 1 / January 2023
- Published online by Cambridge University Press:
- 08 April 2021, pp. 1-69
- Print publication:
- January 2023
-
- Article
- Export citation
The bifurcation locus for numbers of bounded type
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 42 / Issue 7 / July 2022
- Published online by Cambridge University Press:
- 08 April 2021, pp. 2239-2269
- Print publication:
- July 2022
-
- Article
- Export citation
The strong Suslin reciprocity law
- Part of
-
- Journal:
- Compositio Mathematica / Volume 157 / Issue 4 / April 2021
- Published online by Cambridge University Press:
- 01 April 2021, pp. 649-676
- Print publication:
- April 2021
-
- Article
- Export citation
Volume function and Mahler measure of exact polynomials
- Part of
-
- Journal:
- Compositio Mathematica / Volume 157 / Issue 4 / April 2021
- Published online by Cambridge University Press:
- 14 April 2021, pp. 809-834
- Print publication:
- April 2021
-
- Article
- Export citation