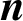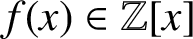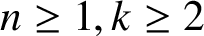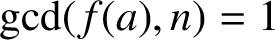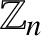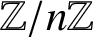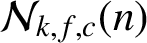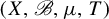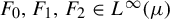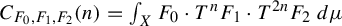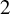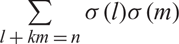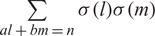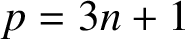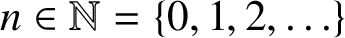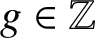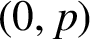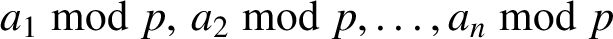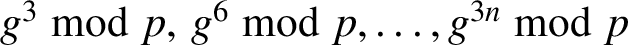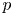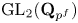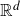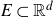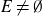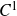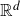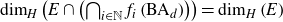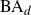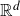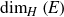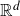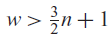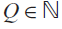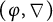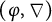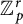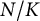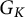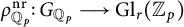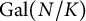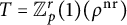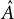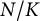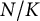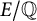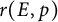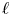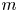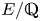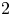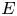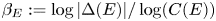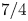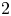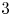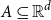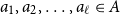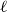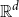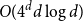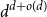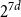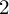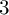Refine listing
Actions for selected content:
2816 results in 11xxx
THE BOREL CHARACTER
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 22 / Issue 2 / March 2023
- Published online by Cambridge University Press:
- 26 July 2021, pp. 747-797
- Print publication:
- March 2023
-
- Article
- Export citation
METRICAL PROBLEMS IN DIOPHANTINE APPROXIMATION
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 104 / Issue 3 / December 2021
- Published online by Cambridge University Press:
- 26 July 2021, pp. 519-521
- Print publication:
- December 2021
-
- Article
-
- You have access
- HTML
- Export citation
ON NONCRITICAL GALOIS REPRESENTATIONS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 22 / Issue 1 / January 2023
- Published online by Cambridge University Press:
- 22 July 2021, pp. 383-420
- Print publication:
- January 2023
-
- Article
- Export citation
SUMS OF POLYNOMIAL-TYPE EXCEPTIONAL UNITS MODULO
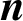 $\boldsymbol {n}$
$\boldsymbol {n}$
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 105 / Issue 2 / April 2022
- Published online by Cambridge University Press:
- 21 July 2021, pp. 202-211
- Print publication:
- April 2022
-
- Article
- Export citation
Multiple correlation sequences not approximable by nilsequences
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 42 / Issue 9 / September 2022
- Published online by Cambridge University Press:
- 16 July 2021, pp. 2711-2722
- Print publication:
- September 2022
-
- Article
- Export citation
EVALUATION OF CONVOLUTION SUMS
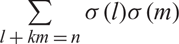 $$\sum\limits_{l + km = n} {\sigma (l)\sigma (m)} $$ AND
$$\sum\limits_{l + km = n} {\sigma (l)\sigma (m)} $$ AND 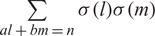 $$\sum\limits_{al + bm = n} {\sigma (l)\sigma (m)} $$ FOR k = a · b = 21, 33, AND 35
$$\sum\limits_{al + bm = n} {\sigma (l)\sigma (m)} $$ FOR k = a · b = 21, 33, AND 35
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 64 / Issue 2 / May 2022
- Published online by Cambridge University Press:
- 16 July 2021, pp. 434-453
- Print publication:
- May 2022
-
- Article
- Export citation
CUBES IN FINITE FIELDS AND RELATED PERMUTATIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 105 / Issue 2 / April 2022
- Published online by Cambridge University Press:
- 15 July 2021, pp. 188-196
- Print publication:
- April 2022
-
- Article
- Export citation
THE GENERIC FIBRE OF MODULI SPACES OF BOUNDED LOCAL G-SHTUKAS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 22 / Issue 2 / March 2023
- Published online by Cambridge University Press:
- 12 July 2021, pp. 799-878
- Print publication:
- March 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Counting and equidistribution in quaternionic Heisenberg groups
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 173 / Issue 1 / July 2022
- Published online by Cambridge University Press:
- 08 July 2021, pp. 67-104
- Print publication:
- July 2022
-
- Article
- Export citation
Diagrams in the mod p cohomology of Shimura curves
- Part of
-
- Journal:
- Compositio Mathematica / Volume 157 / Issue 8 / August 2021
- Published online by Cambridge University Press:
- 07 July 2021, pp. 1653-1723
- Print publication:
- August 2021
-
- Article
- Export citation
Random fractals and their intersection with winning sets
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 172 / Issue 3 / May 2022
- Published online by Cambridge University Press:
- 07 July 2021, pp. 655-684
- Print publication:
- May 2022
-
- Article
- Export citation
QUANTITATIVE ESTIMATE FOR THE MEASURE OF A SET OF REAL NUMBERS
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 64 / Issue 2 / May 2022
- Published online by Cambridge University Press:
- 06 July 2021, pp. 411-433
- Print publication:
- May 2022
-
- Article
- Export citation
A group-theoretic generalization of the p-adic local monodromy theorem
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 74 / Issue 5 / October 2022
- Published online by Cambridge University Press:
- 29 June 2021, pp. 1450-1485
- Print publication:
- October 2022
-
- Article
- Export citation
The epsilon constant conjecture for higher dimensional unramified twists of
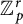 ${\mathbb Z}_p^r$(1)
${\mathbb Z}_p^r$(1)
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 74 / Issue 5 / October 2022
- Published online by Cambridge University Press:
- 29 June 2021, pp. 1405-1449
- Print publication:
- October 2022
-
- Article
- Export citation
An elliptic curve analogue of Pillai’s lower bound on primitive roots
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 65 / Issue 2 / June 2022
- Published online by Cambridge University Press:
- 29 June 2021, pp. 496-505
- Print publication:
- June 2022
-
- Article
- Export citation
The distribution of the maximum of partial sums of Kloosterman sums and other trace functions
- Part of
-
- Journal:
- Compositio Mathematica / Volume 157 / Issue 7 / July 2021
- Published online by Cambridge University Press:
- 28 June 2021, pp. 1610-1651
- Print publication:
- July 2021
-
- Article
- Export citation
Joint Poisson distribution of prime factors in sets
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 173 / Issue 1 / July 2022
- Published online by Cambridge University Press:
- 23 June 2021, pp. 189-200
- Print publication:
- July 2022
-
- Article
- Export citation
Large families of elliptic curves ordered by conductor
- Part of
-
- Journal:
- Compositio Mathematica / Volume 157 / Issue 7 / July 2021
- Published online by Cambridge University Press:
- 22 June 2021, pp. 1538-1583
- Print publication:
- July 2021
-
- Article
- Export citation
On convex holes in d-dimensional point sets
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 31 / Issue 1 / January 2022
- Published online by Cambridge University Press:
- 18 June 2021, pp. 101-108
-
- Article
- Export citation
GEOMETRIC QUADRATIC CHABAUTY
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 22 / Issue 1 / January 2023
- Published online by Cambridge University Press:
- 17 June 2021, pp. 279-333
- Print publication:
- January 2023
-
- Article
-
- You have access
- Open access
- Export citation