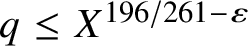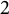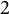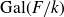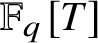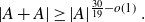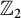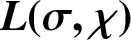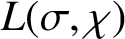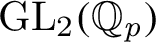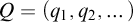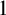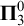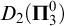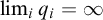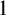Refine listing
Actions for selected content:
2812 results in 11xxx
TRUNCATED AFFINE SPRINGER FIBERS AND ARTHUR’S WEIGHTED ORBITAL INTEGRALS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 22 / Issue 4 / July 2023
- Published online by Cambridge University Press:
- 10 November 2021, pp. 1757-1818
- Print publication:
- July 2023
-
- Article
- Export citation
COUNTEREXAMPLES TO THE HASSE PRINCIPLE IN FAMILIES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 106 / Issue 1 / August 2022
- Published online by Cambridge University Press:
- 05 November 2021, pp. 18-27
- Print publication:
- August 2022
-
- Article
- Export citation
A NOTE ON GIRSTMAIR’S IRREDUCIBILITY CRITERION
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 106 / Issue 1 / August 2022
- Published online by Cambridge University Press:
- 04 November 2021, pp. 62-66
- Print publication:
- August 2022
-
- Article
- Export citation
Corrections to “Value sets of sparse polynomials”
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 65 / Issue 4 / December 2022
- Published online by Cambridge University Press:
- 02 November 2021, pp. 1071-1073
- Print publication:
- December 2022
-
- Article
- Export citation
The essential dimension of congruence covers
- Part of
-
- Journal:
- Compositio Mathematica / Volume 157 / Issue 11 / November 2021
- Published online by Cambridge University Press:
- 27 October 2021, pp. 2407-2432
- Print publication:
- November 2021
-
- Article
- Export citation
Squarefree Integers in Arithmetic Progressions to Smooth Moduli
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 9 / 2021
- Published online by Cambridge University Press:
- 27 October 2021, e72
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A dynamical characterization for monogenity at every level of some infinite
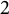 $2$-towers
$2$-towers
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 65 / Issue 3 / September 2022
- Published online by Cambridge University Press:
- 20 October 2021, pp. 806-814
- Print publication:
- September 2022
-
- Article
- Export citation
Congruences for critical values of higher derivatives of twisted Hasse–Weil L-functions, III
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 173 / Issue 2 / September 2022
- Published online by Cambridge University Press:
- 19 October 2021, pp. 431-456
- Print publication:
- September 2022
-
- Article
- Export citation
AUTOMORPHIC LEFSCHETZ PROPERTIES FOR NONCOMPACT ARITHMETIC MANIFOLDS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 22 / Issue 4 / July 2023
- Published online by Cambridge University Press:
- 18 October 2021, pp. 1655-1702
- Print publication:
- July 2023
-
- Article
- Export citation
CONGRUENCES OF SAITO–KUROKAWA LIFTS AND DENOMINATORS OF CENTRAL SPINOR L-VALUES
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 64 / Issue 2 / May 2022
- Published online by Cambridge University Press:
- 14 October 2021, pp. 504-525
- Print publication:
- May 2022
-
- Article
- Export citation
Nonvanishing for cubic L-functions
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 9 / 2021
- Published online by Cambridge University Press:
- 11 October 2021, e69
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A DIMENSIONAL RESULT ON THE PRODUCT OF CONSECUTIVE PARTIAL QUOTIENTS IN CONTINUED FRACTIONS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 113 / Issue 3 / December 2022
- Published online by Cambridge University Press:
- 11 October 2021, pp. 357-385
- Print publication:
- December 2022
-
- Article
- Export citation
An update on the sum-product problem
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 173 / Issue 2 / September 2022
- Published online by Cambridge University Press:
- 11 October 2021, pp. 411-430
- Print publication:
- September 2022
-
- Article
- Export citation
On metabelian 2-class field towers over
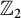 $\mathbb Z_2$-extensions of real quadratic fields
$\mathbb Z_2$-extensions of real quadratic fields
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 65 / Issue 3 / September 2022
- Published online by Cambridge University Press:
- 06 October 2021, pp. 795-805
- Print publication:
- September 2022
-
- Article
- Export citation
A NOTE ON LARGE VALUES OF
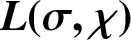 $\boldsymbol{L(\sigma ,\chi )}$
$\boldsymbol{L(\sigma ,\chi )}$
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 105 / Issue 3 / June 2022
- Published online by Cambridge University Press:
- 04 October 2021, pp. 412-418
- Print publication:
- June 2022
-
- Article
- Export citation
ON TRANSCENDENTAL CONTINUED FRACTIONS IN FIELDS OF FORMAL POWER SERIES OVER FINITE FIELDS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 105 / Issue 3 / June 2022
- Published online by Cambridge University Press:
- 01 October 2021, pp. 392-403
- Print publication:
- June 2022
-
- Article
- Export citation
Fine Selmer groups of congruent p-adic Galois representations
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 65 / Issue 3 / September 2022
- Published online by Cambridge University Press:
- 29 September 2021, pp. 702-722
- Print publication:
- September 2022
-
- Article
- Export citation
ON SOME CONSEQUENCES OF A THEOREM OF J. LUDWIG
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 21 / Issue 3 / May 2022
- Published online by Cambridge University Press:
- 27 September 2021, pp. 1067-1106
- Print publication:
- May 2022
-
- Article
-
- You have access
- Open access
- Export citation
DESCRIPTIVE COMPLEXITY IN CANTOR SERIES
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 87 / Issue 3 / September 2022
- Published online by Cambridge University Press:
- 27 September 2021, pp. 1023-1045
- Print publication:
- September 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
An arithmetic property of intertwining operators for p-adic groups
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 75 / Issue 1 / February 2023
- Published online by Cambridge University Press:
- 17 September 2021, pp. 83-107
- Print publication:
- February 2023
-
- Article
- Export citation