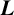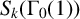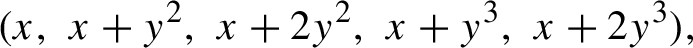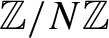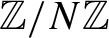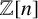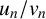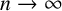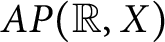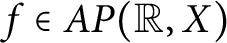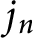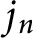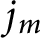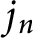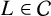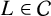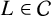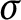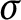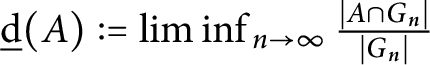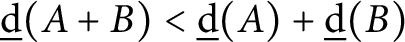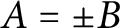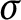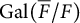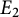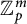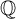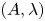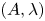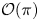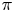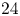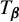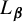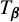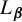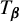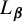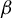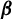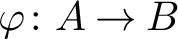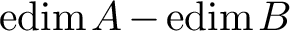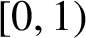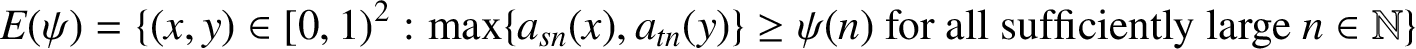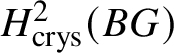Refine listing
Actions for selected content:
2812 results in 11xxx
COUNTING HECKE EIGENFORMS WITH NONVANISHING
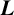 $\boldsymbol {L}$-VALUE
$\boldsymbol {L}$-VALUE
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 106 / Issue 1 / August 2022
- Published online by Cambridge University Press:
- 24 January 2022, pp. 28-47
- Print publication:
- August 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On several notions of complexity of polynomial progressions
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 43 / Issue 4 / April 2023
- Published online by Cambridge University Press:
- 20 January 2022, pp. 1269-1323
- Print publication:
- April 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
APÉRY LIMITS FOR ELLIPTIC
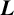 $\boldsymbol {L}$-VALUES
$\boldsymbol {L}$-VALUES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 106 / Issue 2 / October 2022
- Published online by Cambridge University Press:
- 19 January 2022, pp. 273-279
- Print publication:
- October 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A note on spaces of almost periodic functions with values in Banach spaces
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 65 / Issue 4 / December 2022
- Published online by Cambridge University Press:
- 18 January 2022, pp. 953-962
- Print publication:
- December 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On multiplicative energy of subsets of varieties
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 75 / Issue 1 / February 2023
- Published online by Cambridge University Press:
- 13 January 2022, pp. 322-340
- Print publication:
- February 2023
-
- Article
- Export citation
Stieltjes interlacing of the zeros of
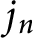 $j_n$
$j_n$
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 65 / Issue 4 / December 2022
- Published online by Cambridge University Press:
- 13 January 2022, pp. 976-993
- Print publication:
- December 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ON STARK’S CLASS NUMBER CONJECTURE AND THE GENERALISED BRAUER–SIEGEL CONJECTURE
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 106 / Issue 2 / October 2022
- Published online by Cambridge University Press:
- 10 January 2022, pp. 288-300
- Print publication:
- October 2022
-
- Article
- Export citation
Kneser’s theorem in
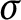 $\sigma $-finite abelian groups
$\sigma $-finite abelian groups
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 65 / Issue 4 / December 2022
- Published online by Cambridge University Press:
- 10 January 2022, pp. 936-942
- Print publication:
- December 2022
-
- Article
- Export citation
POINTS IN A FOLD
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 106 / Issue 1 / August 2022
- Published online by Cambridge University Press:
- 10 January 2022, pp. 7-17
- Print publication:
- August 2022
-
- Article
- Export citation
Euler characteristics and their congruences for multisigned Selmer groups
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 75 / Issue 1 / February 2023
- Published online by Cambridge University Press:
- 10 January 2022, pp. 298-321
- Print publication:
- February 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
EULER PRODUCT ASYMPTOTICS FOR DIRICHLET
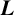 $\boldsymbol {L}$-FUNCTIONS
$\boldsymbol {L}$-FUNCTIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 106 / Issue 1 / August 2022
- Published online by Cambridge University Press:
- 07 January 2022, pp. 48-56
- Print publication:
- August 2022
-
- Article
- Export citation
Hausdorff dimension of the set of almost convergent sequences
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 64 / Issue 3 / September 2022
- Published online by Cambridge University Press:
- 06 January 2022, pp. 691-697
- Print publication:
- September 2022
-
- Article
- Export citation
Faltings height and Néron–Tate height of a theta divisor
- Part of
-
- Journal:
- Compositio Mathematica / Volume 158 / Issue 1 / January 2022
- Published online by Cambridge University Press:
- 24 January 2022, pp. 1-32
- Print publication:
- January 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Some generating functions and inequalities for the andrews–stanley partition functions
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 65 / Issue 1 / February 2022
- Published online by Cambridge University Press:
- 27 December 2021, pp. 120-135
-
- Article
- Export citation
Dynamical behavior of alternate base expansions
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 43 / Issue 3 / March 2023
- Published online by Cambridge University Press:
- 22 December 2021, pp. 827-860
- Print publication:
- March 2023
-
- Article
- Export citation
Uniform perfectness of the Berkovich Julia sets in non-archimedean dynamics
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 173 / Issue 3 / November 2022
- Published online by Cambridge University Press:
- 21 December 2021, pp. 573-590
- Print publication:
- November 2022
-
- Article
- Export citation
A FREENESS CRITERION WITHOUT PATCHING FOR MODULES OVER LOCAL RINGS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 22 / Issue 5 / September 2023
- Published online by Cambridge University Press:
- 20 December 2021, pp. 2117-2129
- Print publication:
- September 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ON THE INCREASING PARTIAL QUOTIENTS OF CONTINUED FRACTIONS OF POINTS IN THE PLANE
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 105 / Issue 3 / June 2022
- Published online by Cambridge University Press:
- 17 December 2021, pp. 404-411
- Print publication:
- June 2022
-
- Article
- Export citation
Dieudonné theory via cohomology of classifying stacks
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 9 / 2021
- Published online by Cambridge University Press:
- 15 December 2021, e81
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
PROOF OF SOME CONJECTURAL CONGRUENCES OF DA SILVA AND SELLERS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 106 / Issue 1 / August 2022
- Published online by Cambridge University Press:
- 13 December 2021, pp. 57-61
- Print publication:
- August 2022
-
- Article
- Export citation