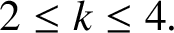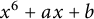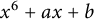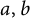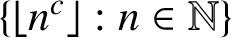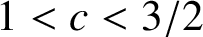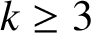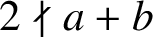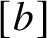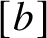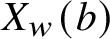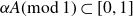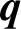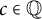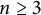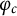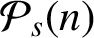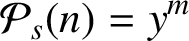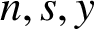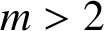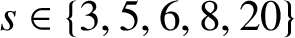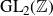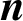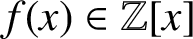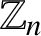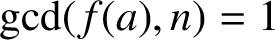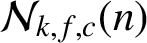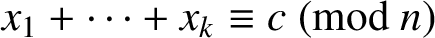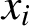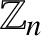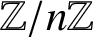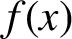Refine listing
Actions for selected content:
2812 results in 11xxx
ON WARING’S PROBLEM IN SUMS OF THREE CUBES FOR SMALLER POWERS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 114 / Issue 3 / June 2023
- Published online by Cambridge University Press:
- 16 September 2021, pp. 378-405
- Print publication:
- June 2023
-
- Article
- Export citation
ON THE MODULARITY OF SOLUTIONS TO CERTAIN DIFFERENTIAL EQUATIONS OF HYPERGEOMETRIC TYPE
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 105 / Issue 3 / June 2022
- Published online by Cambridge University Press:
- 15 September 2021, pp. 385-391
- Print publication:
- June 2022
-
- Article
- Export citation
On nonmonogenic number fields defined by
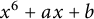 $x^6+ax+b$
$x^6+ax+b$
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 65 / Issue 3 / September 2022
- Published online by Cambridge University Press:
- 15 September 2021, pp. 788-794
- Print publication:
- September 2022
-
- Article
- Export citation
CONSECUTIVE SQUARE-FREE NUMBERS IN PIATETSKI-SHAPIRO SEQUENCES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 105 / Issue 2 / April 2022
- Published online by Cambridge University Press:
- 13 September 2021, pp. 217-222
- Print publication:
- April 2022
-
- Article
- Export citation
ON A PROBLEM OF RICHARD GUY
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 105 / Issue 1 / February 2022
- Published online by Cambridge University Press:
- 13 September 2021, pp. 12-18
- Print publication:
- February 2022
-
- Article
- Export citation
A PROOF OF MERCA’S CONJECTURES ON SUMS OF ODD DIVISOR FUNCTIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 105 / Issue 2 / April 2022
- Published online by Cambridge University Press:
- 10 September 2021, pp. 197-201
- Print publication:
- April 2022
-
- Article
- Export citation
Cordial elements and dimensions of affine Deligne–Lusztig varieties
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 9 / 2021
- Published online by Cambridge University Press:
- 08 September 2021, e9
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
HEDGEHOGS IN LEHMER’S PROBLEM
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 105 / Issue 2 / April 2022
- Published online by Cambridge University Press:
- 07 September 2021, pp. 236-242
- Print publication:
- April 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Remarks about inhomogeneous pair correlations
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 173 / Issue 2 / September 2022
- Published online by Cambridge University Press:
- 06 September 2021, pp. 369-386
- Print publication:
- September 2022
-
- Article
- Export citation
A FAMILY OF
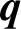 $\boldsymbol {q}$-SUPERCONGRUENCES MODULO THE CUBE OF A CYCLOTOMIC POLYNOMIAL
$\boldsymbol {q}$-SUPERCONGRUENCES MODULO THE CUBE OF A CYCLOTOMIC POLYNOMIAL
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 105 / Issue 2 / April 2022
- Published online by Cambridge University Press:
- 03 September 2021, pp. 296-302
- Print publication:
- April 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A generalized Davenport expansion
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 64 / Issue 3 / August 2021
- Published online by Cambridge University Press:
- 26 August 2021, pp. 711-715
-
- Article
- Export citation
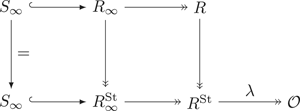
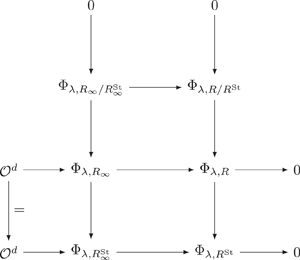
Wiles defect for Hecke algebras that are not complete intersections
- Part of
-
- Journal:
- Compositio Mathematica / Volume 157 / Issue 9 / September 2021
- Published online by Cambridge University Press:
- 16 August 2021, pp. 2046-2088
- Print publication:
- September 2021
-
- Article
- Export citation
Some results on the Flynn–Poonen–Schaefer conjecture
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 65 / Issue 3 / September 2022
- Published online by Cambridge University Press:
- 11 August 2021, pp. 598-611
- Print publication:
- September 2022
-
- Article
- Export citation
The classification of free algebras of orthogonal modular forms
- Part of
-
- Journal:
- Compositio Mathematica / Volume 157 / Issue 9 / September 2021
- Published online by Cambridge University Press:
- 06 August 2021, pp. 2026-2045
- Print publication:
- September 2021
-
- Article
- Export citation
A UNIQUE PERFECT POWER DECAGONAL NUMBER
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 105 / Issue 2 / April 2022
- Published online by Cambridge University Press:
- 06 August 2021, pp. 212-216
- Print publication:
- April 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A positive proportion of locally soluble quartic Thue equations are globally insoluble
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 173 / Issue 2 / September 2022
- Published online by Cambridge University Press:
- 05 August 2021, pp. 333-348
- Print publication:
- September 2022
-
- Article
- Export citation
THE BOREL CHARACTER
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 22 / Issue 2 / March 2023
- Published online by Cambridge University Press:
- 26 July 2021, pp. 747-797
- Print publication:
- March 2023
-
- Article
- Export citation
METRICAL PROBLEMS IN DIOPHANTINE APPROXIMATION
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 104 / Issue 3 / December 2021
- Published online by Cambridge University Press:
- 26 July 2021, pp. 519-521
- Print publication:
- December 2021
-
- Article
-
- You have access
- HTML
- Export citation
ON NONCRITICAL GALOIS REPRESENTATIONS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 22 / Issue 1 / January 2023
- Published online by Cambridge University Press:
- 22 July 2021, pp. 383-420
- Print publication:
- January 2023
-
- Article
- Export citation
SUMS OF POLYNOMIAL-TYPE EXCEPTIONAL UNITS MODULO
 $\boldsymbol {n}$
$\boldsymbol {n}$
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 105 / Issue 2 / April 2022
- Published online by Cambridge University Press:
- 21 July 2021, pp. 202-211
- Print publication:
- April 2022
-
- Article
- Export citation