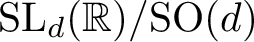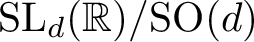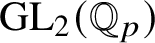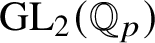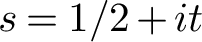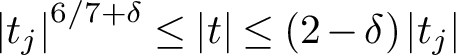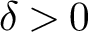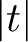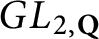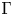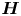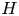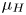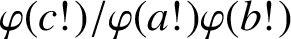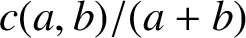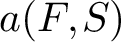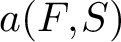Refine listing
Actions for selected content:
2812 results in 11xxx
QUANTUM ERGODICITY FOR COMPACT QUOTIENTS OF
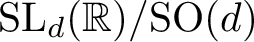 $\operatorname {SL}_d({\mathbb R})/\textrm {SO}(d)$ IN THE BENJAMINI–SCHRAMM LIMIT
$\operatorname {SL}_d({\mathbb R})/\textrm {SO}(d)$ IN THE BENJAMINI–SCHRAMM LIMIT
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 22 / Issue 5 / September 2023
- Published online by Cambridge University Press:
- 13 December 2021, pp. 2075-2115
- Print publication:
- September 2023
-
- Article
- Export citation
Arithmetic derivatives through geometry of numbers
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 65 / Issue 4 / December 2022
- Published online by Cambridge University Press:
- 10 December 2021, pp. 906-923
- Print publication:
- December 2022
-
- Article
- Export citation
AN EFFECTIVE ANALYTIC FORMULA FOR THE NUMBER OF DISTINCT IRREDUCIBLE FACTORS OF A POLYNOMIAL
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 113 / Issue 3 / December 2022
- Published online by Cambridge University Press:
- 09 December 2021, pp. 339-356
- Print publication:
- December 2022
-
- Article
- Export citation
Finiteness properties of the category of mod p representations of
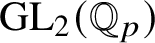 ${\textrm {GL}}_2 (\mathbb {Q}_{p})$
${\textrm {GL}}_2 (\mathbb {Q}_{p})$
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 9 / 2021
- Published online by Cambridge University Press:
- 09 December 2021, e80
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
MOMENTS AND HYBRID SUBCONVEXITY FOR SYMMETRIC-SQUARE L-FUNCTIONS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 22 / Issue 5 / September 2023
- Published online by Cambridge University Press:
- 06 December 2021, pp. 2029-2073
- Print publication:
- September 2023
-
- Article
- Export citation
ON HIGHER DIMENSIONAL ARITHMETIC PROGRESSIONS IN MEYER SETS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 114 / Issue 3 / June 2023
- Published online by Cambridge University Press:
- 06 December 2021, pp. 312-336
- Print publication:
- June 2023
-
- Article
- Export citation
Eisenstein metrics
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 75 / Issue 3 / June 2023
- Published online by Cambridge University Press:
- 03 December 2021, pp. 778-803
- Print publication:
- June 2023
-
- Article
- Export citation
SZEMERÉDI’S THEOREM: AN EXPLORATION OF IMPURITY, EXPLANATION, AND CONTENT
- Part of
-
- Journal:
- The Review of Symbolic Logic / Volume 16 / Issue 3 / September 2023
- Published online by Cambridge University Press:
- 03 December 2021, pp. 700-739
- Print publication:
- September 2023
-
- Article
- Export citation
Special curves in modular surfaces
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 1 / March 2023
- Published online by Cambridge University Press:
- 02 December 2021, pp. 1-18
- Print publication:
- March 2023
-
- Article
- Export citation
Corrigendum: Generic rank of Betti map and unlikely intersections
- Part of
-
- Journal:
- Compositio Mathematica / Volume 157 / Issue 12 / December 2021
- Published online by Cambridge University Press:
- 05 January 2022, pp. 2747-2748
- Print publication:
- December 2021
-
- Article
-
- You have access
- HTML
- Export citation
TWISTED DOUBLING INTEGRALS FOR BRYLINSKI–DELIGNE EXTENSIONS OF CLASSICAL GROUPS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 22 / Issue 4 / July 2023
- Published online by Cambridge University Press:
- 01 December 2021, pp. 1931-1985
- Print publication:
- July 2023
-
- Article
- Export citation
Translates of homogeneous measures associated with observable subgroups on some homogeneous spaces
- Part of
-
- Journal:
- Compositio Mathematica / Volume 157 / Issue 12 / December 2021
- Published online by Cambridge University Press:
- 22 December 2021, pp. 2657-2698
- Print publication:
- December 2021
-
- Article
- Export citation
A blurred view of Van der Waerden type theorems
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 31 / Issue 4 / July 2022
- Published online by Cambridge University Press:
- 26 November 2021, pp. 684-701
-
- Article
- Export citation
DENSITY-LIKE AND GENERALIZED DENSITY IDEALS
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 87 / Issue 1 / March 2022
- Published online by Cambridge University Press:
- 23 November 2021, pp. 228-251
- Print publication:
- March 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
NOTES ON THE DPRM PROPERTY FOR LISTABLE STRUCTURES
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 87 / Issue 1 / March 2022
- Published online by Cambridge University Press:
- 23 November 2021, pp. 273-312
- Print publication:
- March 2022
-
- Article
- Export citation
A restaurant process with cocktail bar and relations to the three-parameter Mittag–Leffler distribution
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 58 / Issue 4 / December 2021
- Published online by Cambridge University Press:
- 22 November 2021, pp. 978-1006
- Print publication:
- December 2021
-
- Article
- Export citation
TIGHT UNIVERSAL TRIANGULAR FORMS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 105 / Issue 3 / June 2022
- Published online by Cambridge University Press:
- 18 November 2021, pp. 372-384
- Print publication:
- June 2022
-
- Article
- Export citation
ON QUOTIENTS OF VALUES OF EULER’S FUNCTION ON FACTORIALS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 105 / Issue 3 / June 2022
- Published online by Cambridge University Press:
- 17 November 2021, pp. 353-364
- Print publication:
- June 2022
-
- Article
- Export citation
GEOMETRIC WEIGHT-SHIFTING OPERATORS ON HILBERT MODULAR FORMS IN CHARACTERISTIC p
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 22 / Issue 4 / July 2023
- Published online by Cambridge University Press:
- 15 November 2021, pp. 1871-1930
- Print publication:
- July 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ON FUNDAMENTAL FOURIER COEFFICIENTS OF SIEGEL CUSP FORMS OF DEGREE 2
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 22 / Issue 4 / July 2023
- Published online by Cambridge University Press:
- 12 November 2021, pp. 1819-1869
- Print publication:
- July 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation