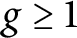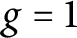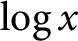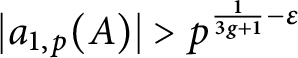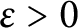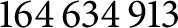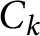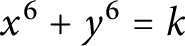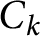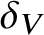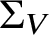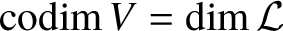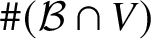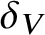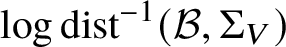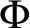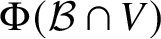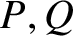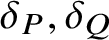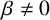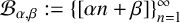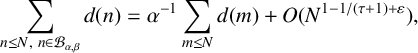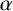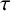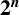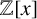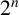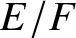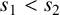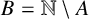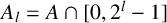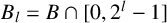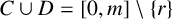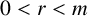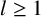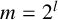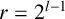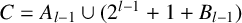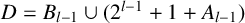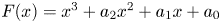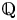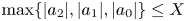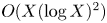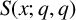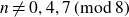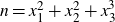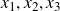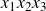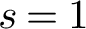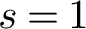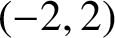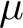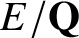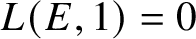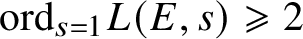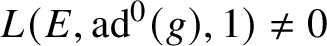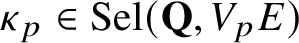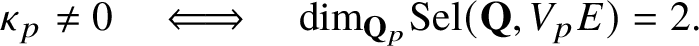Refine listing
Actions for selected content:
2812 results in 11xxx
Bounds for the distribution of the Frobenius traces associated to products of non-CM elliptic curves
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 75 / Issue 3 / June 2023
- Published online by Cambridge University Press:
- 07 March 2022, pp. 687-712
- Print publication:
- June 2023
-
- Article
- Export citation
Integers that are sums of two rational sixth powers
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 1 / March 2023
- Published online by Cambridge University Press:
- 07 March 2022, pp. 166-177
- Print publication:
- March 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Point counting for foliations over number fields
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 10 / 2022
- Published online by Cambridge University Press:
- 04 March 2022, e6
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ON THE DIVISOR FUNCTION OVER NONHOMOGENEOUS BEATTY SEQUENCES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 106 / Issue 2 / October 2022
- Published online by Cambridge University Press:
- 04 March 2022, pp. 280-287
- Print publication:
- October 2022
-
- Article
- Export citation
RECIPROCAL MONOGENIC QUINTINOMIALS OF DEGREE
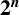 $\boldsymbol {2^n}$
$\boldsymbol {2^n}$
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 106 / Issue 3 / December 2022
- Published online by Cambridge University Press:
- 04 March 2022, pp. 437-447
- Print publication:
- December 2022
-
- Article
- Export citation
Chow groups and L-derivatives of automorphic motives for unitary groups, II.
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 10 / 2022
- Published online by Cambridge University Press:
- 04 March 2022, e5
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Dilogarithm identities after Bridgeman
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 174 / Issue 1 / January 2023
- Published online by Cambridge University Press:
- 03 March 2022, pp. 1-23
- Print publication:
- January 2023
-
- Article
- Export citation
ON INTEGER SETS WITH THE SAME REPRESENTATION FUNCTIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 106 / Issue 2 / October 2022
- Published online by Cambridge University Press:
- 03 March 2022, pp. 224-235
- Print publication:
- October 2022
-
- Article
- Export citation
On monic abelian cubics
- Part of
-
- Journal:
- Compositio Mathematica / Volume 158 / Issue 3 / March 2022
- Published online by Cambridge University Press:
- 16 May 2022, pp. 550-567
- Print publication:
- March 2022
-
- Article
- Export citation
Trace and Künneth formulas for singularity categories and applications
- Part of
-
- Journal:
- Compositio Mathematica / Volume 158 / Issue 3 / March 2022
- Published online by Cambridge University Press:
- 03 June 2022, pp. 483-528
- Print publication:
- March 2022
-
- Article
- Export citation
DISTRIBUTION OF ELEMENTS OF A FLOOR FUNCTION SET IN ARITHMETICAL PROGRESSIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 106 / Issue 3 / December 2022
- Published online by Cambridge University Press:
- 01 March 2022, pp. 419-424
- Print publication:
- December 2022
-
- Article
- Export citation
Uniform bounds for norms of theta series and arithmetic applications
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 173 / Issue 3 / November 2022
- Published online by Cambridge University Press:
- 28 February 2022, pp. 669-691
- Print publication:
- November 2022
-
- Article
- Export citation
VALUES OF ZETA FUNCTIONS OF ARITHMETIC SURFACES AT
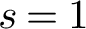 $s=1$
$s=1$
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 22 / Issue 5 / September 2023
- Published online by Cambridge University Press:
- 28 February 2022, pp. 2455-2496
- Print publication:
- September 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Sums of random multiplicative functions over function fields with few irreducible factors
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 173 / Issue 3 / November 2022
- Published online by Cambridge University Press:
- 28 February 2022, pp. 715-726
- Print publication:
- November 2022
-
- Article
- Export citation
DIOPHANTINE EQUATIONS FOR POLYNOMIALS WITH RESTRICTED COEFFICIENTS, I (POWER VALUES)
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 106 / Issue 2 / October 2022
- Published online by Cambridge University Press:
- 22 February 2022, pp. 254-263
- Print publication:
- October 2022
-
- Article
- Export citation
LOWER-ORDER TERMS OF THE ONE-LEVEL DENSITY OF A FAMILY OF QUADRATIC HECKE
 $\boldsymbol {L}$-FUNCTIONS
$\boldsymbol {L}$-FUNCTIONS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 114 / Issue 2 / April 2023
- Published online by Cambridge University Press:
- 22 February 2022, pp. 178-221
- Print publication:
- April 2023
-
- Article
- Export citation
ON THE GEOMETRY OF THE PAPPAS–RAPOPORT MODELS FOR PEL SHIMURA VARIETIES
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 22 / Issue 5 / September 2023
- Published online by Cambridge University Press:
- 18 February 2022, pp. 2403-2445
- Print publication:
- September 2023
-
- Article
- Export citation
INDIVISIBILITY OF HEEGNER CYCLES OVER SHIMURA CURVES AND SELMER GROUPS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 22 / Issue 5 / September 2023
- Published online by Cambridge University Press:
- 15 February 2022, pp. 2297-2336
- Print publication:
- September 2023
-
- Article
- Export citation
On the nonvanishing of generalised Kato classes for elliptic curves of rank 2
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 10 / 2022
- Published online by Cambridge University Press:
- 15 February 2022, e12
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
THE p-ADIC GROSS–ZAGIER FORMULA ON SHIMURA CURVES, II: NONSPLIT PRIMES
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 22 / Issue 5 / September 2023
- Published online by Cambridge University Press:
- 15 February 2022, pp. 2199-2240
- Print publication:
- September 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation