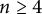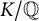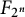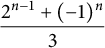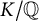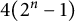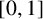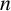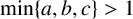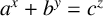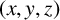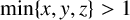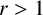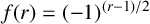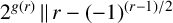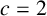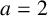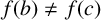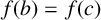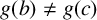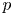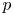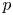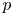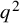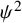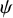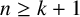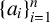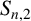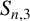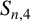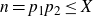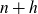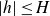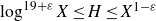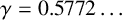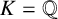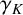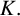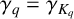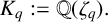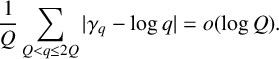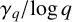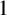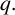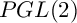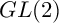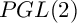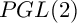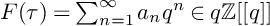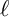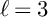Refine listing
Actions for selected content:
2812 results in 11xxx
Vertices of the Harder and Narasimhan polygons and the laws of large numbers
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 1 / March 2023
- Published online by Cambridge University Press:
- 14 June 2022, pp. 340-357
- Print publication:
- March 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Arithmetically equivalent fields in a Galois extension with Frobenius Galois group of 2-power degree
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 2 / June 2023
- Published online by Cambridge University Press:
- 13 June 2022, pp. 380-394
- Print publication:
- June 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
BINARY SIGNED-DIGIT REPRESENTATIONS IN PAPERFOLDING
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 106 / Issue 3 / December 2022
- Published online by Cambridge University Press:
- 10 June 2022, pp. 363-375
- Print publication:
- December 2022
-
- Article
- Export citation
A NOTE ON THE NUMBER OF SOLUTIONS OF TERNARY PURELY EXPONENTIAL DIOPHANTINE EQUATIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 107 / Issue 1 / February 2023
- Published online by Cambridge University Press:
- 10 June 2022, pp. 53-65
- Print publication:
- February 2023
-
- Article
- Export citation
Sum expressions for Kubota–Leopoldt $p$
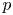 -adic $L$
-adic $L$ -functions
-functions
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 65 / Issue 2 / May 2022
- Published online by Cambridge University Press:
- 10 June 2022, pp. 460-479
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Joint ergodicity of fractional powers of primes
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 10 / 2022
- Published online by Cambridge University Press:
- 09 June 2022, e30
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Some cases of Kudla’s modularity conjecture for unitary Shimura varieties
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 10 / 2022
- Published online by Cambridge University Press:
- 09 June 2022, e37
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Motohashi’s formula for the fourth moment of individual Dirichlet L-functions and applications
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 10 / 2022
- Published online by Cambridge University Press:
- 09 June 2022, e41
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A SHARP UPPER BOUND FOR THE SUM OF RECIPROCALS OF LEAST COMMON MULTIPLES II
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 107 / Issue 1 / February 2023
- Published online by Cambridge University Press:
- 09 June 2022, pp. 10-21
- Print publication:
- February 2023
-
- Article
- Export citation
Correlations of almost primes
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 174 / Issue 2 / March 2023
- Published online by Cambridge University Press:
- 09 June 2022, pp. 301-344
- Print publication:
- March 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On elliptic curves with p-isogenies over quadratic fields
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 75 / Issue 3 / June 2023
- Published online by Cambridge University Press:
- 07 June 2022, pp. 945-964
- Print publication:
- June 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Geometric orbital integrals and the center of the enveloping algebra
- Part of
-
- Journal:
- Compositio Mathematica / Volume 158 / Issue 6 / June 2022
- Published online by Cambridge University Press:
- 11 August 2022, pp. 1189-1253
- Print publication:
- June 2022
-
- Article
- Export citation
Uniform Properties of Ideals in Rings of Restricted Power Series
- Part of
-
- Journal:
- Bulletin of Symbolic Logic / Volume 28 / Issue 2 / June 2022
- Published online by Cambridge University Press:
- 28 June 2022, p. 258
- Print publication:
- June 2022
-
- Article
-
- You have access
- HTML
- Export citation
EULER–KRONECKER CONSTANTS FOR CYCLOTOMIC FIELDS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 107 / Issue 1 / February 2023
- Published online by Cambridge University Press:
- 30 May 2022, pp. 79-84
- Print publication:
- February 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
SELMER GROUPS OF ELLIPTIC CURVES OVER THE
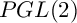 $PGL(2)$ EXTENSION
$PGL(2)$ EXTENSION
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 248 / December 2022
- Published online by Cambridge University Press:
- 30 May 2022, pp. 922-938
- Print publication:
- December 2022
-
- Article
- Export citation
MAGNETIC (QUASI-)MODULAR FORMS
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 248 / December 2022
- Published online by Cambridge University Press:
- 30 May 2022, pp. 849-864
- Print publication:
- December 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
DETERMINACY OF SCHMIDT’S GAME AND OTHER INTERSECTION GAMES
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 88 / Issue 1 / March 2023
- Published online by Cambridge University Press:
- 30 May 2022, pp. 1-21
- Print publication:
- March 2023
-
- Article
- Export citation
THE BOUNDARY OF THE p-RANK
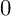 $0$ STRATUM OF THE MODULI SPACE OF CYCLIC COVERS OF THE PROJECTIVE LINE
$0$ STRATUM OF THE MODULI SPACE OF CYCLIC COVERS OF THE PROJECTIVE LINE
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 248 / December 2022
- Published online by Cambridge University Press:
- 30 May 2022, pp. 865-887
- Print publication:
- December 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On the Kottwitz conjecture for local shtuka spaces
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 10 / 2022
- Published online by Cambridge University Press:
- 26 May 2022, e13
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Tropical moments of tropical Jacobians
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 75 / Issue 4 / August 2023
- Published online by Cambridge University Press:
- 24 May 2022, pp. 1045-1075
- Print publication:
- August 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation