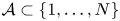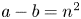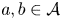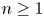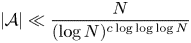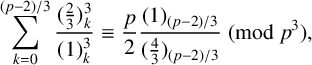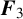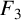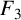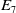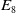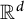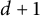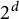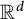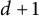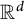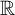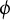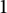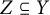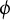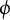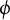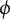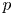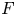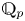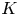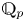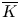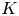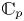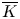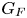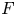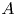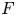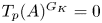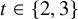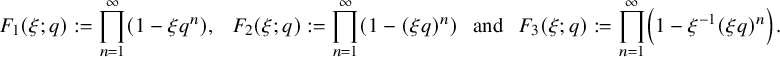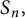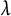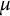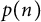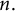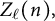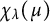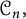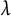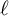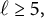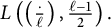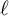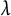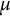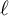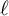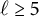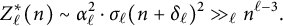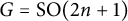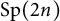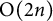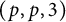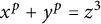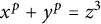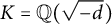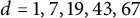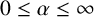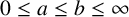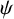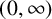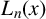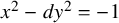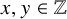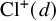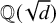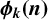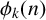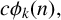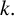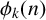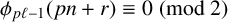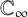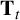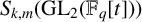Refine listing
Actions for selected content:
2812 results in 11xxx
A new upper bound for sets with no square differences
- Part of
-
- Journal:
- Compositio Mathematica / Volume 158 / Issue 8 / August 2022
- Published online by Cambridge University Press:
- 30 September 2022, pp. 1777-1798
- Print publication:
- August 2022
-
- Article
- Export citation
On the Hardy–Littlewood–Chowla conjecture on average
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 10 / 2022
- Published online by Cambridge University Press:
- 27 July 2022, e57
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A
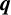 $\boldsymbol {q}$-SUPERCONGRUENCE MODULO THE THIRD POWER OF A CYCLOTOMIC POLYNOMIAL
$\boldsymbol {q}$-SUPERCONGRUENCE MODULO THE THIRD POWER OF A CYCLOTOMIC POLYNOMIAL
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 106 / Issue 2 / October 2022
- Published online by Cambridge University Press:
- 18 July 2022, pp. 236-242
- Print publication:
- October 2022
-
- Article
- Export citation
New lower bounds for van der Waerden numbers
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 10 / 2022
- Published online by Cambridge University Press:
- 13 July 2022, e18
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A GENERALISATION OF A SUPERCONGRUENCE ON THE TRUNCATED APPELL SERIES
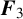 $\boldsymbol F_3$
$\boldsymbol F_3$
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 107 / Issue 2 / April 2023
- Published online by Cambridge University Press:
- 13 July 2022, pp. 296-303
- Print publication:
- April 2023
-
- Article
- Export citation
TIGHT UNIVERSAL SUMS OF m-GONAL NUMBERS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 107 / Issue 1 / February 2023
- Published online by Cambridge University Press:
- 13 July 2022, pp. 40-52
- Print publication:
- February 2023
-
- Article
- Export citation
Enriques surfaces and an Apollonian packing in eight dimensions
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 65 / Issue 1 / January 2023
- Published online by Cambridge University Press:
- 11 July 2022, pp. 205-221
- Print publication:
- January 2023
-
- Article
- Export citation
On the general dyadic grids on
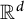 ${\mathbb {R}}^d$
${\mathbb {R}}^d$
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 75 / Issue 4 / August 2023
- Published online by Cambridge University Press:
- 08 July 2022, pp. 1147-1175
- Print publication:
- August 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A conjecture strengthening the Zariski dense orbit problem for birational maps of dynamical degree one
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 2 / June 2023
- Published online by Cambridge University Press:
- 07 July 2022, pp. 477-491
- Print publication:
- June 2023
-
- Article
- Export citation
On p-adic uniformization of abelian varieties with good reduction
- Part of
-
- Journal:
- Compositio Mathematica / Volume 158 / Issue 7 / July 2022
- Published online by Cambridge University Press:
- 05 September 2022, pp. 1449-1476
- Print publication:
- July 2022
-
- Article
- Export citation
MODEL THEORY OF GALOIS ACTIONS OF TORSION ABELIAN GROUPS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 22 / Issue 6 / November 2023
- Published online by Cambridge University Press:
- 30 June 2022, pp. 2943-2985
- Print publication:
- November 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Distributions on partitions arising from Hilbert schemes and hook lengths
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 10 / 2022
- Published online by Cambridge University Press:
- 29 June 2022, e49
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Zeros in the character tables of symmetric groups with an
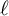 $\ell $-core index
$\ell $-core index
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 2 / June 2023
- Published online by Cambridge University Press:
- 27 June 2022, pp. 467-476
- Print publication:
- June 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The Gelfand–Graev representation of classical groups in terms of Hecke algebras
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 75 / Issue 4 / August 2023
- Published online by Cambridge University Press:
- 24 June 2022, pp. 1343-1368
- Print publication:
- August 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On ternary Diophantine equations of signature
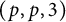 $(p,p,\text{3})$ over number fields
$(p,p,\text{3})$ over number fields
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 75 / Issue 4 / August 2023
- Published online by Cambridge University Press:
- 24 June 2022, pp. 1293-1313
- Print publication:
- August 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ON LÜROTH EXPANSIONS IN WHICH THE LARGEST DIGIT GROWS WITH SLOWLY INCREASING SPEED
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 107 / Issue 2 / April 2023
- Published online by Cambridge University Press:
- 23 June 2022, pp. 204-214
- Print publication:
- April 2023
-
- Article
- Export citation
The second moment of
 $\mathrm {GL}(n)\times \mathrm {GL}(n)$ Rankin–Selberg L-functions
$\mathrm {GL}(n)\times \mathrm {GL}(n)$ Rankin–Selberg L-functions
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 10 / 2022
- Published online by Cambridge University Press:
- 23 June 2022, e47
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The 8-rank of the narrow class group and the negative Pell equation
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 10 / 2022
- Published online by Cambridge University Press:
- 21 June 2022, e46
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ON THE PARITY OF THE GENERALISED FROBENIUS PARTITION FUNCTIONS
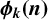 $\boldsymbol {\phi _k(n)}$
$\boldsymbol {\phi _k(n)}$
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 106 / Issue 3 / December 2022
- Published online by Cambridge University Press:
- 15 June 2022, pp. 431-436
- Print publication:
- December 2022
-
- Article
- Export citation
HECKE OPERATORS AND DRINFELD CUSP FORMS OF LEVEL
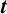 $\boldsymbol {t}$
$\boldsymbol {t}$
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 107 / Issue 2 / April 2023
- Published online by Cambridge University Press:
- 15 June 2022, pp. 184-195
- Print publication:
- April 2023
-
- Article
- Export citation