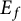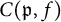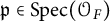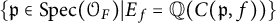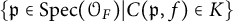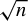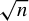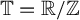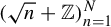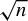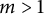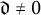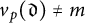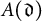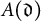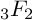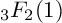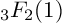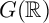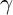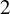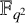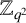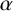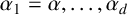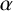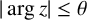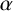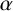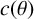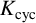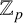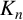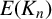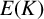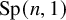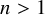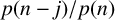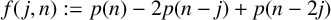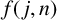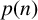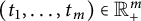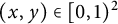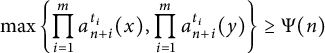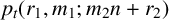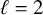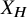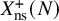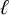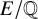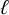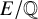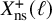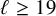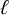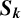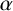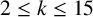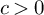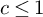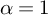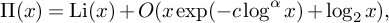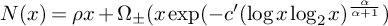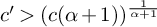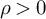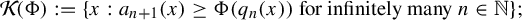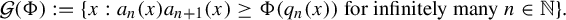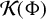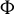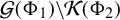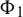Refine listing
Actions for selected content:
2812 results in 11xxx
On generation of the coefficient field of a primitive Hilbert modular form by a single Fourier coefficient
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 2 / June 2023
- Published online by Cambridge University Press:
- 08 September 2022, pp. 587-598
- Print publication:
- June 2023
-
- Article
- Export citation
Rational points on nonlinear horocycles and pigeonhole statistics for the fractional parts of
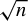 $\sqrt {n}$
$\sqrt {n}$
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 43 / Issue 9 / September 2023
- Published online by Cambridge University Press:
- 08 September 2022, pp. 3108-3130
- Print publication:
- September 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Modular forms and some cases of the Inverse Galois Problem
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 2 / June 2023
- Published online by Cambridge University Press:
- 06 September 2022, pp. 568-586
- Print publication:
- June 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The shape of cyclic number fields
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 2 / June 2023
- Published online by Cambridge University Press:
- 06 September 2022, pp. 599-609
- Print publication:
- June 2023
-
- Article
- Export citation
EVALUATION OF CERTAIN EXOTIC
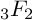 $_3F_2$(1)-SERIES
$_3F_2$(1)-SERIES
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 249 / March 2023
- Published online by Cambridge University Press:
- 05 September 2022, pp. 107-118
- Print publication:
- March 2023
-
- Article
- Export citation
GENERALIZED ZETA INTEGRALS ON CERTAIN REAL PREHOMOGENEOUS VECTOR SPACES
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 249 / March 2023
- Published online by Cambridge University Press:
- 05 September 2022, pp. 50-87
- Print publication:
- March 2023
-
- Article
- Export citation
Analytic torsion for log-Enriques surfaces and Borcherds product
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 10 / 2022
- Published online by Cambridge University Press:
- 02 September 2022, e77
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ON LINEARISED POLYNOMIALS, SIDON ARRAYS AND FAST CONSTRUCTION OF SIDON SETS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 106 / Issue 3 / December 2022
- Published online by Cambridge University Press:
- 30 August 2022, pp. 376-384
- Print publication:
- December 2022
-
- Article
- Export citation
AN ANALOGUE OF THE SCHUR–SIEGEL–SMYTH TRACE PROBLEM
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 107 / Issue 2 / April 2023
- Published online by Cambridge University Press:
- 30 August 2022, pp. 227-238
- Print publication:
- April 2023
-
- Article
- Export citation
REMARKS ON HILBERT’S TENTH PROBLEM AND THE IWASAWA THEORY OF ELLIPTIC CURVES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 107 / Issue 3 / June 2023
- Published online by Cambridge University Press:
- 30 August 2022, pp. 440-450
- Print publication:
- June 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Truncated versions of three identities of Euler and Gauss
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 65 / Issue 3 / August 2022
- Published online by Cambridge University Press:
- 30 August 2022, pp. 775-798
-
- Article
- Export citation
Quaternionic hyperbolic lattices of minimal covolume
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 10 / 2022
- Published online by Cambridge University Press:
- 25 August 2022, e68
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
THE SECOND SHIFTED DIFFERENCE OF PARTITIONS AND ITS APPLICATIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 107 / Issue 1 / February 2023
- Published online by Cambridge University Press:
- 25 August 2022, pp. 66-78
- Print publication:
- February 2023
-
- Article
- Export citation
A note on the relative growth of products of multiple partial quotients in the plane
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 2 / June 2023
- Published online by Cambridge University Press:
- 19 August 2022, pp. 544-552
- Print publication:
- June 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Shintani lifts of nearly holomorphic modular forms
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 75 / Issue 5 / October 2023
- Published online by Cambridge University Press:
- 19 August 2022, pp. 1446-1492
- Print publication:
- October 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ON THE NUMBER OF 2-HOOKS AND 3-HOOKS OF INTEGER PARTITIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 107 / Issue 3 / June 2023
- Published online by Cambridge University Press:
- 18 August 2022, pp. 432-439
- Print publication:
- June 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
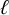 $\ell $-adic images of Galois for elliptic curves over
$\ell $-adic images of Galois for elliptic curves over  $\mathbb {Q}$ (and an appendix with John Voight)
$\mathbb {Q}$ (and an appendix with John Voight)
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 10 / 2022
- Published online by Cambridge University Press:
- 12 August 2022, e62
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
THE ABSOLUTE
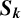 $\boldsymbol {S_k}$-MEASURE OF TOTALLY POSITIVE ALGEBRAIC INTEGERS
$\boldsymbol {S_k}$-MEASURE OF TOTALLY POSITIVE ALGEBRAIC INTEGERS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 107 / Issue 2 / April 2023
- Published online by Cambridge University Press:
- 11 August 2022, pp. 239-249
- Print publication:
- April 2023
-
- Article
- Export citation
THE OPTIMAL MALLIAVIN-TYPE REMAINDER FOR BEURLING GENERALIZED INTEGERS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 23 / Issue 1 / January 2024
- Published online by Cambridge University Press:
- 09 August 2022, pp. 249-278
- Print publication:
- January 2024
-
- Article
- Export citation
Hausdorff dimension of Dirichlet non-improvable set versus well-approximable set
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 43 / Issue 8 / August 2023
- Published online by Cambridge University Press:
- 04 August 2022, pp. 2707-2731
- Print publication:
- August 2023
-
- Article
- Export citation