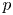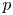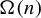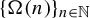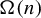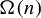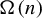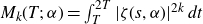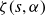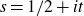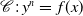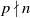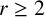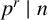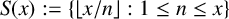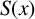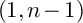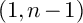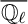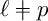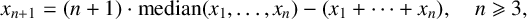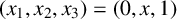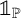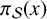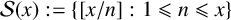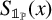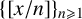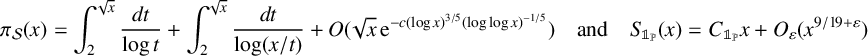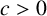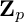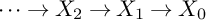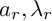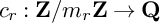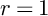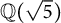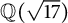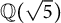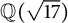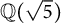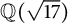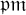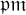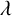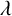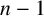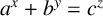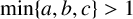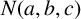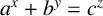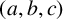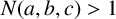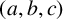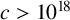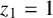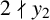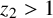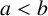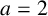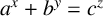Refine listing
Actions for selected content:
2812 results in 11xxx
A
 $p$-adic monodromy theorem for de Rham local systems
$p$-adic monodromy theorem for de Rham local systems
- Part of
-
- Journal:
- Compositio Mathematica / Volume 158 / Issue 12 / December 2022
- Published online by Cambridge University Press:
- 15 December 2022, pp. 2157-2205
- Print publication:
- December 2022
-
- Article
- Export citation
A dynamical approach to the asymptotic behavior of the sequence
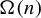 $\Omega (n)$
$\Omega (n)$
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 43 / Issue 11 / November 2023
- Published online by Cambridge University Press:
- 29 November 2022, pp. 3685-3706
- Print publication:
- November 2023
-
- Article
- Export citation
Moments of the Hurwitz zeta function on the critical line
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 174 / Issue 3 / May 2023
- Published online by Cambridge University Press:
- 28 November 2022, pp. 631-661
- Print publication:
- May 2023
-
- Article
- Export citation
Most numbers are not normal
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 175 / Issue 1 / July 2023
- Published online by Cambridge University Press:
- 28 November 2022, pp. 1-11
- Print publication:
- July 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Galois representations of superelliptic curves
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 65 / Issue 2 / May 2023
- Published online by Cambridge University Press:
- 24 November 2022, pp. 356-382
- Print publication:
- May 2023
-
- Article
- Export citation
DISTRIBUTION OF r-FREE INTEGERS OVER A FLOOR FUNCTION SET
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 108 / Issue 1 / August 2023
- Published online by Cambridge University Press:
- 23 November 2022, pp. 107-113
- Print publication:
- August 2023
-
- Article
- Export citation
COHOMOLOGY OF THE BRUHAT–TITS STRATA IN THE UNRAMIFIED UNITARY RAPOPORT–ZINK SPACE OF SIGNATURE
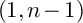 $(1,n-1)$
$(1,n-1)$
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 250 / June 2023
- Published online by Cambridge University Press:
- 23 November 2022, pp. 470-497
- Print publication:
- June 2023
-
- Article
- Export citation
THE AKIYAMA MEAN-MEDIAN MAP HAS UNBOUNDED TRANSIT TIME AND DISCONTINUOUS LIMIT
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 108 / Issue 2 / October 2023
- Published online by Cambridge University Press:
- 23 November 2022, pp. 298-307
- Print publication:
- October 2023
-
- Article
- Export citation
ON THE PRIMES IN FLOOR FUNCTION SETS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 108 / Issue 2 / October 2023
- Published online by Cambridge University Press:
- 23 November 2022, pp. 236-243
- Print publication:
- October 2023
-
- Article
- Export citation
IWASAWA THEORY FOR p-TORSION CLASS GROUP SCHEMES IN CHARACTERISTIC p
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 250 / June 2023
- Published online by Cambridge University Press:
- 22 November 2022, pp. 298-351
- Print publication:
- June 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Generating function of multiple polylog of Hurwitz type
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 76 / Issue 1 / February 2024
- Published online by Cambridge University Press:
- 21 November 2022, pp. 1-17
- Print publication:
- February 2024
-
- Article
- Export citation
Fermat’s Last Theorem over
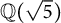 $\mathbb {Q}(\sqrt {\text{5}})$ and
$\mathbb {Q}(\sqrt {\text{5}})$ and 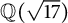 $\mathbb {Q}(\sqrt {\text{17}})$
$\mathbb {Q}(\sqrt {\text{17}})$
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 76 / Issue 1 / February 2024
- Published online by Cambridge University Press:
- 21 November 2022, pp. 18-38
- Print publication:
- February 2024
-
- Article
- Export citation
NOTES ON ATKIN–LEHNER THEORY FOR DRINFELD MODULAR FORMS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 108 / Issue 1 / August 2023
- Published online by Cambridge University Press:
- 15 November 2022, pp. 50-68
- Print publication:
- August 2023
-
- Article
- Export citation
Basic loci of Coxeter type with arbitrary parahoric level
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 76 / Issue 1 / February 2024
- Published online by Cambridge University Press:
- 14 November 2022, pp. 126-172
- Print publication:
- February 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
OVERCONVERGENT DE RHAM EICHLER–SHIMURA MORPHISMS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 23 / Issue 2 / March 2024
- Published online by Cambridge University Press:
- 14 November 2022, pp. 647-703
- Print publication:
- March 2024
-
- Article
- Export citation
ON THE NUMBER OF NEARLY SELF-CONJUGATE PARTITIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 108 / Issue 1 / August 2023
- Published online by Cambridge University Press:
- 11 November 2022, pp. 114-119
- Print publication:
- August 2023
-
- Article
- Export citation
ON A CONJECTURE CONCERNING THE NUMBER OF SOLUTIONS TO
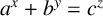 $a^x+b^y=c^z$
$a^x+b^y=c^z$
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 108 / Issue 1 / August 2023
- Published online by Cambridge University Press:
- 11 November 2022, pp. 40-49
- Print publication:
- August 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
OHNO–ZAGIER TYPE RELATIONS FOR MULTIPLE t-VALUES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 107 / Issue 2 / April 2023
- Published online by Cambridge University Press:
- 11 November 2022, pp. 215-226
- Print publication:
- April 2023
-
- Article
- Export citation
INTEGRAL POINTS ON SINGULAR DEL PEZZO SURFACES
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 23 / Issue 3 / May 2024
- Published online by Cambridge University Press:
- 10 November 2022, pp. 1259-1294
- Print publication:
- May 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
AN AMAZING IDENTITY OF GAUSS AND JENKINS’ LEMMA
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 108 / Issue 1 / August 2023
- Published online by Cambridge University Press:
- 08 November 2022, pp. 86-98
- Print publication:
- August 2023
-
- Article
- Export citation