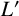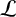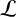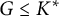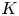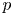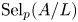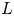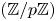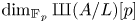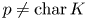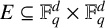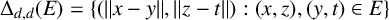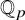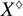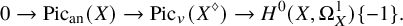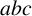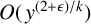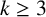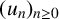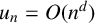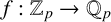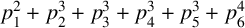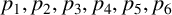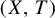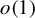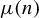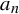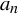Refine listing
Actions for selected content:
2812 results in 11xxx
A NOTE ON MÖBIUS DISJOINTNESS FOR SKEW PRODUCTS ON A CIRCLE AND A NILMANIFOLD
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 107 / Issue 3 / June 2023
- Published online by Cambridge University Press:
- 04 October 2022, pp. 471-482
- Print publication:
- June 2023
-
- Article
- Export citation
ERDŐS–LIOUVILLE SETS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 107 / Issue 2 / April 2023
- Published online by Cambridge University Press:
- 03 October 2022, pp. 284-289
- Print publication:
- April 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
APPROXIMATING NUMBERS OF THE CANTOR SET BY ALGEBRAIC NUMBERS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 107 / Issue 2 / April 2023
- Published online by Cambridge University Press:
- 03 October 2022, pp. 196-203
- Print publication:
- April 2023
-
- Article
- Export citation
D-finite multivariate series with arithmetic restrictions on their coefficients
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 75 / Issue 6 / December 2023
- Published online by Cambridge University Press:
- 03 October 2022, pp. 1745-1779
- Print publication:
- December 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The growth of Tate–Shafarevich groups in cyclic extensions
- Part of
-
- Journal:
- Compositio Mathematica / Volume 158 / Issue 10 / October 2022
- Published online by Cambridge University Press:
- 04 November 2022, pp. 2014-2032
- Print publication:
- October 2022
-
- Article
- Export citation
ON THE TWO-PARAMETER ERDŐS–FALCONER DISTANCE PROBLEM IN FINITE FIELDS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 107 / Issue 3 / June 2023
- Published online by Cambridge University Press:
- 29 September 2022, pp. 502-506
- Print publication:
- June 2023
-
- Article
- Export citation
PONTRYAGIN DUALITY FOR VARIETIES OVER p-ADIC FIELDS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 23 / Issue 1 / January 2024
- Published online by Cambridge University Press:
- 28 September 2022, pp. 425-462
- Print publication:
- January 2024
-
- Article
- Export citation
Exceptional jumps of Picard ranks of reductions of K3 surfaces over number fields
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 10 / 2022
- Published online by Cambridge University Press:
- 26 September 2022, e21
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
THE PAUCITY PROBLEM FOR CERTAIN SYMMETRIC DIOPHANTINE EQUATIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 108 / Issue 1 / August 2023
- Published online by Cambridge University Press:
- 23 September 2022, pp. 29-39
- Print publication:
- August 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Line bundles on rigid spaces in the v-topology
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 10 / 2022
- Published online by Cambridge University Press:
- 22 September 2022, e82
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Effective bounds on differences of singular moduli that are S-units
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 174 / Issue 2 / March 2023
- Published online by Cambridge University Press:
- 22 September 2022, pp. 415-450
- Print publication:
- March 2023
-
- Article
- Export citation
ON THE EUCLIDEAN ALGORITHM: RHYTHM WITHOUT RECURSION
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 107 / Issue 3 / June 2023
- Published online by Cambridge University Press:
- 22 September 2022, pp. 361-367
- Print publication:
- June 2023
-
- Article
- Export citation
A NOTE ON POWERFUL NUMBERS IN SHORT INTERVALS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 108 / Issue 1 / August 2023
- Published online by Cambridge University Press:
- 22 September 2022, pp. 99-106
- Print publication:
- August 2023
-
- Article
- Export citation
ON p-ADIC INTERPOLATION IN TWO OF MAHLER’S PROBLEMS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 108 / Issue 1 / August 2023
- Published online by Cambridge University Press:
- 22 September 2022, pp. 69-80
- Print publication:
- August 2023
-
- Article
- Export citation
SINGULAR DIRECTIONS IN VEECH SURFACES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 107 / Issue 3 / June 2023
- Published online by Cambridge University Press:
- 16 September 2022, pp. 390-397
- Print publication:
- June 2023
-
- Article
- Export citation
SPACINGS BETWEEN SELECTED PRIME DIVISORS OF AN INTEGER
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 107 / Issue 3 / June 2023
- Published online by Cambridge University Press:
- 15 September 2022, pp. 403-415
- Print publication:
- June 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A NOTE ON AN ASYMPTOTIC VERSION OF A PROBLEM OF MAHLER
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 107 / Issue 3 / June 2023
- Published online by Cambridge University Press:
- 15 September 2022, pp. 398-402
- Print publication:
- June 2023
-
- Article
- Export citation
ON THE WARING–GOLDBACH PROBLEM FOR ONE SQUARE, FOUR CUBES AND ONE BIQUADRATE
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 107 / Issue 3 / June 2023
- Published online by Cambridge University Press:
- 15 September 2022, pp. 416-431
- Print publication:
- June 2023
-
- Article
- Export citation
Omega results for cubic field counts via lower-order terms in the one-level density
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 10 / 2022
- Published online by Cambridge University Press:
- 15 September 2022, e80
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Arbitrarily slow decay in the Möbius disjointness conjecture
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 43 / Issue 9 / September 2023
- Published online by Cambridge University Press:
- 09 September 2022, pp. 2863-2880
- Print publication:
- September 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation