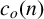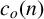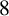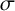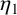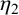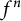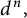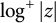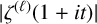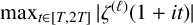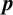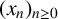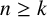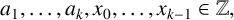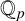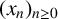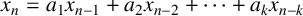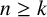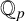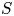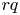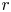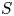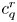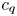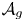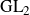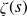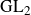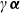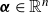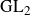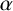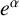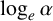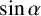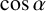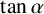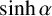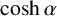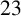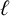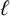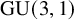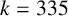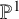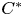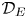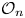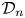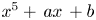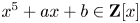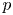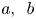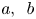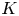Refine listing
Actions for selected content:
2812 results in 11xxx
ON AN AVERAGE GOLDBACH REPRESENTATION FORMULA OF FUJII
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 250 / June 2023
- Published online by Cambridge University Press:
- 17 January 2023, pp. 511-532
- Print publication:
- June 2023
-
- Article
- Export citation
PROOF OF A CONJECTURE OF BANERJEE AND DASTIDAR ON ODD CRANK
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 108 / Issue 3 / December 2023
- Published online by Cambridge University Press:
- 13 January 2023, pp. 406-411
- Print publication:
- December 2023
-
- Article
- Export citation
ON THE NUMBER OF ALGEBRAIC POINTS ON THE GRAPH OF THE WEIERSTRASS SIGMA FUNCTIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 108 / Issue 2 / October 2023
- Published online by Cambridge University Press:
- 13 January 2023, pp. 205-216
- Print publication:
- October 2023
-
- Article
- Export citation
ZERO DENSITY THEOREMS FOR FAMILIES OF DIRICHLET L-FUNCTIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 108 / Issue 2 / October 2023
- Published online by Cambridge University Press:
- 13 January 2023, pp. 224-235
- Print publication:
- October 2023
-
- Article
- Export citation
Mahler measure of polynomial iterates
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 3 / September 2023
- Published online by Cambridge University Press:
- 12 January 2023, pp. 881-885
- Print publication:
- September 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A NOTE ON THE LARGE VALUES OF
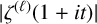 $|\zeta ^{(\ell )}(1+{i}t)|$
$|\zeta ^{(\ell )}(1+{i}t)|$
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 108 / Issue 2 / October 2023
- Published online by Cambridge University Press:
- 05 January 2023, pp. 217-223
- Print publication:
- October 2023
-
- Article
- Export citation
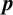 $\boldsymbol {p}$-ADIC QUOTIENT SETS: LINEAR RECURRENCE SEQUENCES
$\boldsymbol {p}$-ADIC QUOTIENT SETS: LINEAR RECURRENCE SEQUENCES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 108 / Issue 1 / August 2023
- Published online by Cambridge University Press:
- 05 January 2023, pp. 19-28
- Print publication:
- August 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Equidistribution of Hodge loci II
- Part of
-
- Journal:
- Compositio Mathematica / Volume 159 / Issue 1 / January 2023
- Published online by Cambridge University Press:
- 12 January 2023, pp. 1-52
- Print publication:
- January 2023
-
- Article
- Export citation
A zero density estimate and fractional imaginary parts of zeros for
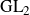 $\textrm{GL}_2$ L-functions
$\textrm{GL}_2$ L-functions
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 174 / Issue 3 / May 2023
- Published online by Cambridge University Press:
- 28 December 2022, pp. 605-630
- Print publication:
- May 2023
-
- Article
- Export citation
SIN, COS, EXP AND LOG OF LIOUVILLE NUMBERS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 108 / Issue 1 / August 2023
- Published online by Cambridge University Press:
- 23 December 2022, pp. 81-85
- Print publication:
- August 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
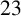 $23$-REGULAR PARTITIONS AND MODULAR FORMS WITH COMPLEX MULTIPLICATION
$23$-REGULAR PARTITIONS AND MODULAR FORMS WITH COMPLEX MULTIPLICATION
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 108 / Issue 2 / October 2023
- Published online by Cambridge University Press:
- 23 December 2022, pp. 254-263
- Print publication:
- October 2023
-
- Article
- Export citation
NORMAL AND IRREDUCIBLE ADIC SPACES, THE OPENNESS OF FINITE MORPHISMS, AND A STEIN FACTORIZATION
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 250 / June 2023
- Published online by Cambridge University Press:
- 16 December 2022, pp. 498-510
- Print publication:
- June 2023
-
- Article
- Export citation
Iwasawa–Greenberg main conjecture for nonordinary modular forms and Eisenstein congruences on GU(3,1)
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 10 / 2022
- Published online by Cambridge University Press:
- 15 December 2022, e110
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A PAIR OF EQUATIONS IN EIGHT PRIME CUBES AND POWERS OF 2
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 108 / Issue 2 / October 2023
- Published online by Cambridge University Press:
- 14 December 2022, pp. 244-253
- Print publication:
- October 2023
-
- Article
- Export citation
Local newforms for the general linear groups over a non-archimedean local field
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 10 / 2022
- Published online by Cambridge University Press:
- 13 December 2022, e24
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
SUPER CATALAN NUMBERS AND FOURIER SUMMATIONS OVER FINITE FIELDS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 107 / Issue 1 / February 2023
- Published online by Cambridge University Press:
- 12 December 2022, p. 170
- Print publication:
- February 2023
-
- Article
-
- You have access
- HTML
- Export citation
ON THE FIBRES OF AN ELLIPTIC SURFACE WHERE THE RANK DOES NOT JUMP
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 108 / Issue 2 / October 2023
- Published online by Cambridge University Press:
- 12 December 2022, pp. 276-282
- Print publication:
- October 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On conjugacy of subalgebras in graph C*-algebras. II
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 65 / Issue 4 / November 2022
- Published online by Cambridge University Press:
- 09 December 2022, pp. 1162-1182
-
- Article
- Export citation
SPECIAL VALUES OF ZETA-FUNCTIONS OF REGULAR SCHEMES
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 23 / Issue 1 / January 2024
- Published online by Cambridge University Press:
- 06 December 2022, pp. 495-519
- Print publication:
- January 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Common index divisor of the number fields defined by $x^5+\,ax\,+b$
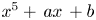
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 65 / Issue 4 / November 2022
- Published online by Cambridge University Press:
- 01 December 2022, pp. 1147-1161
-
- Article
- Export citation