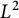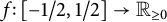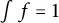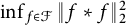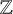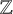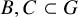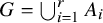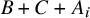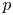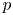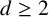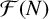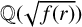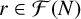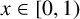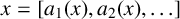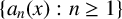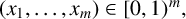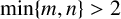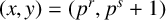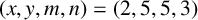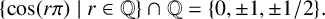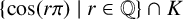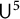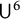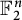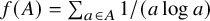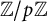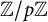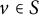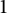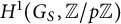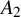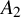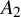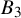Refine listing
Actions for selected content:
2838 results in 11xxx
TRANSCENDENCE OF GENERALISED EULER–KRONECKER CONSTANTS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 109 / Issue 3 / June 2024
- Published online by Cambridge University Press:
- 10 July 2023, pp. 464-470
- Print publication:
- June 2024
-
- Article
- Export citation
INFINITE SERIES CONCERNING HARMONIC NUMBERS AND QUINTIC CENTRAL BINOMIAL COEFFICIENTS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 109 / Issue 2 / April 2024
- Published online by Cambridge University Press:
- 07 July 2023, pp. 225-241
- Print publication:
- April 2024
-
- Article
- Export citation
An optimal
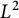 $L^2$ autoconvolution inequality
$L^2$ autoconvolution inequality
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 67 / Issue 1 / March 2024
- Published online by Cambridge University Press:
- 05 July 2023, pp. 108-121
- Print publication:
- March 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Bohr sets in sumsets II: countable abelian groups
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 03 July 2023, e57
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On the u∞-torsion submodule of prismatic cohomology
- Part of
-
- Journal:
- Compositio Mathematica / Volume 159 / Issue 8 / August 2023
- Published online by Cambridge University Press:
- 30 June 2023, pp. 1607-1672
- Print publication:
- August 2023
-
- Article
- Export citation
Kudla–Rapoport conjecture for Krämer models
- Part of
-
- Journal:
- Compositio Mathematica / Volume 159 / Issue 8 / August 2023
- Published online by Cambridge University Press:
- 29 June 2023, pp. 1673-1740
- Print publication:
- August 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ON QUADRATIC FIELDS GENERATED BY POLYNOMIALS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 109 / Issue 3 / June 2024
- Published online by Cambridge University Press:
- 29 June 2023, pp. 476-485
- Print publication:
- June 2024
-
- Article
- Export citation
Finite subgroups of automorphisms of K3 surfaces
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 27 June 2023, e54
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ON THE SHORTEST DISTANCE FUNCTION IN CONTINUED FRACTIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 109 / Issue 2 / April 2024
- Published online by Cambridge University Press:
- 23 June 2023, pp. 186-195
- Print publication:
- April 2024
-
- Article
- Export citation
A NOTE ON THE GOORMAGHTIGH EQUATION CONCERNING DIFFERENCE SETS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 109 / Issue 3 / June 2024
- Published online by Cambridge University Press:
- 23 June 2023, pp. 443-452
- Print publication:
- June 2024
-
- Article
- Export citation
EXPLICIT ESTIMATES FOR THE DISTRIBUTION OF PRIMES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 108 / Issue 2 / October 2023
- Published online by Cambridge University Press:
- 22 June 2023, pp. 341-342
- Print publication:
- October 2023
-
- Article
-
- You have access
- HTML
- Export citation
A DYNAMICAL SYSTEM PROOF OF NIVEN’S THEOREM AND ITS EXTENSIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 109 / Issue 1 / February 2024
- Published online by Cambridge University Press:
- 21 June 2023, pp. 138-151
- Print publication:
- February 2024
-
- Article
- Export citation
Smooth numbers with few nonzero binary digits
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 67 / Issue 1 / March 2024
- Published online by Cambridge University Press:
- 20 June 2023, pp. 74-89
- Print publication:
- March 2024
-
- Article
- Export citation
LEFT AND RIGHT EIGENVECTORS OF A VARIANT OF THE SYLVESTER–KAC MATRIX
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 109 / Issue 2 / April 2024
- Published online by Cambridge University Press:
- 19 June 2023, pp. 316-326
- Print publication:
- April 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Quantitative inverse theorem for Gowers uniformity norms
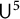 $\mathsf {U}^5$ and
$\mathsf {U}^5$ and 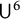 $\mathsf {U}^6$ in
$\mathsf {U}^6$ in 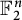 $\mathbb {F}_2^n$
$\mathbb {F}_2^n$
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 76 / Issue 4 / August 2024
- Published online by Cambridge University Press:
- 15 June 2023, pp. 1289-1338
- Print publication:
- August 2024
-
- Article
- Export citation
A proof of the Erdős primitive set conjecture
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 11 / 2023
- Published online by Cambridge University Press:
- 14 June 2023, e18
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On tame
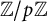 ${\mathbb {Z}}/p{\mathbb {Z}}$-extensions with prescribed ramification
${\mathbb {Z}}/p{\mathbb {Z}}$-extensions with prescribed ramification
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 67 / Issue 1 / March 2024
- Published online by Cambridge University Press:
- 13 June 2023, pp. 40-48
- Print publication:
- March 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On Sarnak’s Density Conjecture and Its Applications
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 13 June 2023, e48
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
THE DIAGONAL CYCLE EULER SYSTEM FOR
 $\mathrm {GL}_2\times \mathrm {GL}_2$
$\mathrm {GL}_2\times \mathrm {GL}_2$
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 24 / Issue 5 / September 2025
- Published online by Cambridge University Press:
- 13 June 2023, pp. 1591-1653
- Print publication:
- September 2025
-
- Article
- Export citation
q-deformed rational numbers and the 2-Calabi–Yau category of type
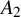 $A_{2}$
$A_{2}$
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 12 June 2023, e47
-
- Article
-
- You have access
- Open access
- HTML
- Export citation