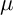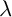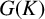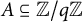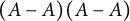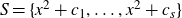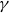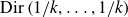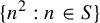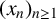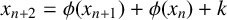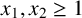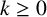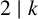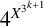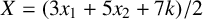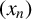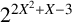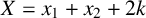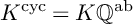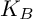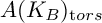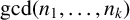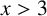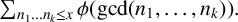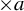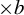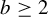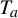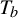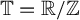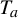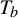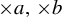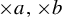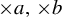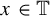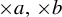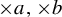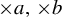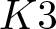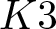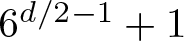Refine listing
Actions for selected content:
2812 results in 11xxx
On theorems of Fermat, Wilson, and Gegenbauer
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 67 / Issue 2 / June 2024
- Published online by Cambridge University Press:
- 12 September 2023, pp. 304-317
- Print publication:
- June 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ON THE DISTRIBUTION OF IWASAWA INVARIANTS ASSOCIATED TO MULTIGRAPHS
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 253 / March 2024
- Published online by Cambridge University Press:
- 08 September 2023, pp. 48-90
- Print publication:
- March 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
THE MORDELL–LANG CONJECTURE FOR SEMIABELIAN VARIETIES DEFINED OVER FIELDS OF POSITIVE CHARACTERISTIC
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 109 / Issue 2 / April 2024
- Published online by Cambridge University Press:
- 08 September 2023, pp. 254-264
- Print publication:
- April 2024
-
- Article
- Export citation
On some multiplicative properties of large difference sets
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 76 / Issue 5 / October 2024
- Published online by Cambridge University Press:
- 08 September 2023, pp. 1538-1555
- Print publication:
- October 2024
-
- Article
- Export citation
Galois groups and prime divisors in random quadratic sequences
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 176 / Issue 1 / January 2024
- Published online by Cambridge University Press:
- 07 September 2023, pp. 95-122
- Print publication:
- January 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Dirichlet law for factorisation of integers, polynomials and permutations
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 175 / Issue 3 / November 2023
- Published online by Cambridge University Press:
- 06 September 2023, pp. 649-676
- Print publication:
- November 2023
-
- Article
- Export citation
Hodge classes and the Jacquet–Langlands correspondence
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 11 / 2023
- Published online by Cambridge University Press:
- 06 September 2023, e22
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
An approximation formula for the shifted cubic moment of automorphic L-functions in the weight aspect
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 77 / Issue 3 / June 2025
- Published online by Cambridge University Press:
- 06 September 2023, pp. 715-738
- Print publication:
- June 2025
-
- Article
- Export citation
A set of 2-recurrence whose perfect squares do not form a set of measurable recurrence
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 6 / June 2024
- Published online by Cambridge University Press:
- 04 September 2023, pp. 1541-1580
- Print publication:
- June 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
AN IMPROVEMENT TO A THEOREM OF LEONETTI AND LUCA
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 109 / Issue 3 / June 2024
- Published online by Cambridge University Press:
- 01 September 2023, pp. 437-442
- Print publication:
- June 2024
-
- Article
- Export citation
ON THE ESSENTIAL TORSION FINITENESS OF ABELIAN VARIETIES OVER TORSION FIELDS
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 253 / March 2024
- Published online by Cambridge University Press:
- 24 August 2023, pp. 91-127
- Print publication:
- March 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Equidistribution of exponential sums indexed by a subgroup of fixed cardinality
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 176 / Issue 1 / January 2024
- Published online by Cambridge University Press:
- 24 August 2023, pp. 65-94
- Print publication:
- January 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ON SUMS INVOLVING THE EULER TOTIENT FUNCTION
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 109 / Issue 3 / June 2024
- Published online by Cambridge University Press:
- 24 August 2023, pp. 486-497
- Print publication:
- June 2024
-
- Article
- Export citation
New mock theta functions and formulas for basic hypergeometric series
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 66 / Issue 3 / August 2023
- Published online by Cambridge University Press:
- 22 August 2023, pp. 868-896
-
- Article
- Export citation
Disjoint hypercyclicity, Sidon sets and weakly mixing operators
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 5 / May 2024
- Published online by Cambridge University Press:
- 22 August 2023, pp. 1315-1329
- Print publication:
- May 2024
-
- Article
- Export citation
Connected components of affine Deligne–Lusztig varieties for unramified groups
- Part of
-
- Journal:
- Compositio Mathematica / Volume 159 / Issue 10 / October 2023
- Published online by Cambridge University Press:
- 17 August 2023, pp. 2051-2088
- Print publication:
- October 2023
-
- Article
- Export citation
Weil Sums over Small Subgroups
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 176 / Issue 1 / January 2024
- Published online by Cambridge University Press:
- 15 August 2023, pp. 39-53
- Print publication:
- January 2024
-
- Article
- Export citation
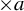 $\times a$ and
$\times a$ and 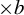 $\times b$ empirical measures, the irregular set and entropy
$\times b$ empirical measures, the irregular set and entropy
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 6 / June 2024
- Published online by Cambridge University Press:
- 15 August 2023, pp. 1673-1692
- Print publication:
- June 2024
-
- Article
- Export citation
Exact formulae and Turán inequalities for Vafa–Witten invariants of
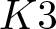 $K3$ surfaces
$K3$ surfaces
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 66 / Issue 3 / August 2023
- Published online by Cambridge University Press:
- 08 August 2023, pp. 845-861
-
- Article
- Export citation
Every Salem number is a difference of two Pisot numbers
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 66 / Issue 3 / August 2023
- Published online by Cambridge University Press:
- 08 August 2023, pp. 862-867
-
- Article
-
- You have access
- Open access
- HTML
- Export citation