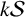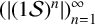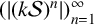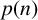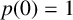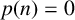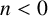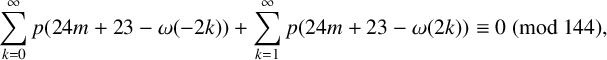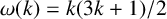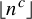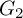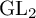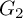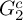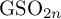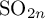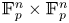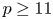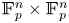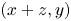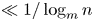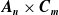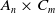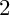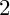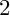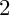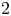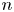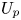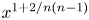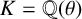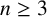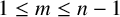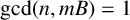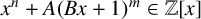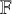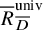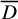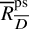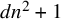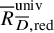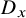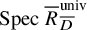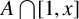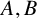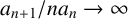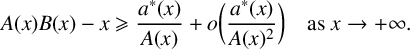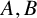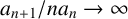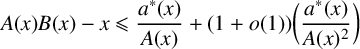Refine listing
Actions for selected content:
2838 results in 11xxx
On the root of unity ambiguity in a formula for the Brumer–Stark units
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 67 / Issue 3 / September 2024
- Published online by Cambridge University Press:
- 27 December 2023, pp. 611-623
- Print publication:
- September 2024
-
- Article
- Export citation
COUNTING UNIONS OF SCHREIER SETS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 110 / Issue 1 / August 2024
- Published online by Cambridge University Press:
- 27 December 2023, pp. 19-31
- Print publication:
- August 2024
-
- Article
- Export citation
DIVISIBILITY OF SUMS OF PARTITION NUMBERS BY MULTIPLES OF 2 AND 3
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 110 / Issue 2 / October 2024
- Published online by Cambridge University Press:
- 22 December 2023, pp. 271-279
- Print publication:
- October 2024
-
- Article
- Export citation
A NOTE ON THE ZEROS OF L-FUNCTIONS ASSOCIATED TO FIXED-ORDER DIRICHLET CHARACTERS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 110 / Issue 2 / October 2024
- Published online by Cambridge University Press:
- 18 December 2023, pp. 252-261
- Print publication:
- October 2024
-
- Article
- Export citation
Bracket words along Hardy field sequences
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 9 / September 2024
- Published online by Cambridge University Press:
- 14 December 2023, pp. 2621-2648
- Print publication:
- September 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
COUNTING DISCRETE, LEVEL-
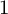 $1$, QUATERNIONIC AUTOMORPHIC REPRESENTATIONS ON
$1$, QUATERNIONIC AUTOMORPHIC REPRESENTATIONS ON 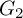 $G_2$
$G_2$
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 23 / Issue 5 / September 2024
- Published online by Cambridge University Press:
- 13 December 2023, pp. 2127-2157
- Print publication:
- September 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
GALOIS REPRESENTATIONS FOR EVEN GENERAL SPECIAL ORTHOGONAL GROUPS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 23 / Issue 5 / September 2024
- Published online by Cambridge University Press:
- 13 December 2023, pp. 1959-2050
- Print publication:
- September 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
NEW EFFECTIVE RESULTS IN THE THEORY OF THE RIEMANN ZETA-FUNCTION
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 109 / Issue 2 / April 2024
- Published online by Cambridge University Press:
- 12 December 2023, pp. 403-406
- Print publication:
- April 2024
-
- Article
-
- You have access
- HTML
- Export citation
Subsets of
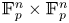 $\mathbb {F}_p^n\times \mathbb {F}_p^n$ without L-shaped configurations
$\mathbb {F}_p^n\times \mathbb {F}_p^n$ without L-shaped configurations
- Part of
-
- Journal:
- Compositio Mathematica / Volume 160 / Issue 1 / January 2024
- Published online by Cambridge University Press:
- 04 December 2023, pp. 176-236
- Print publication:
- January 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ON A COMPARISON BETWEEN DWORK AND RIGID COHOMOLOGIES OF PROJECTIVE COMPLEMENTS
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 254 / June 2024
- Published online by Cambridge University Press:
- 01 December 2023, pp. 420-461
- Print publication:
- June 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Finite orbits for large groups of automorphisms of projective surfaces
- Part of
-
- Journal:
- Compositio Mathematica / Volume 160 / Issue 1 / January 2024
- Published online by Cambridge University Press:
- 30 November 2023, pp. 120-175
- Print publication:
- January 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Partitions with parts separated by parity: conjugation, congruences and the mock theta functions
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 155 / Issue 3 / June 2025
- Published online by Cambridge University Press:
- 30 November 2023, pp. 954-974
- Print publication:
- June 2025
-
- Article
- Export citation
On
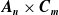 $\boldsymbol{A}_{\boldsymbol{n}} \times \boldsymbol{C}_{\boldsymbol{m}}$-unramified extensions over imaginary quadratic fields
$\boldsymbol{A}_{\boldsymbol{n}} \times \boldsymbol{C}_{\boldsymbol{m}}$-unramified extensions over imaginary quadratic fields
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 66 / Issue 1 / January 2024
- Published online by Cambridge University Press:
- 29 November 2023, pp. 119-125
- Print publication:
- January 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
GENUS
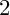 $2$ CURVES WITH BAD REDUCTION AT ONE ODD PRIME
$2$ CURVES WITH BAD REDUCTION AT ONE ODD PRIME
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 254 / June 2024
- Published online by Cambridge University Press:
- 29 November 2023, pp. 498-512
- Print publication:
- June 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
HIGHER MOMENT FORMULAE AND LIMITING DISTRIBUTIONS OF LATTICE POINTS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 23 / Issue 5 / September 2024
- Published online by Cambridge University Press:
- 28 November 2023, pp. 2081-2125
- Print publication:
- September 2024
-
- Article
- Export citation
Slopes in eigenvarieties for definite unitary groups
- Part of
-
- Journal:
- Compositio Mathematica / Volume 160 / Issue 1 / January 2024
- Published online by Cambridge University Press:
- 22 November 2023, pp. 52-89
- Print publication:
- January 2024
-
- Article
- Export citation
ON A CONJECTURE OF LENNY JONES ABOUT CERTAIN MONOGENIC POLYNOMIALS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 110 / Issue 1 / August 2024
- Published online by Cambridge University Press:
- 21 November 2023, pp. 72-76
- Print publication:
- August 2024
-
- Article
- Export citation
Equidimensionality of universal pseudodeformation rings in characteristic p for absolute Galois groups of p-adic fields
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 17 November 2023, e102
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Generalized divisor functions in arithmetic progressions: II
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 67 / Issue 1 / February 2024
- Published online by Cambridge University Press:
- 16 November 2023, pp. 28-56
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ADDITIVE COMPLETION OF THIN SETS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 109 / Issue 3 / June 2024
- Published online by Cambridge University Press:
- 15 November 2023, pp. 429-436
- Print publication:
- June 2024
-
- Article
- Export citation