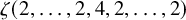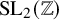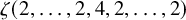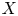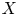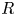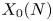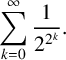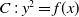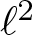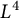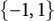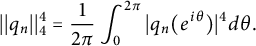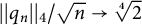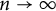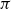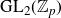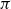Refine listing
Actions for selected content:
2837 results in 11xxx
Summation formulae of multiplicative functions over arithmetic progressions and applications
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 77 / Issue 4 / August 2025
- Published online by Cambridge University Press:
- 12 April 2024, pp. 1243-1270
- Print publication:
- August 2025
-
- Article
- Export citation
GENERALISED QUADRATIC FORMS OVER TOTALLY REAL NUMBER FIELDS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 23 / Issue 6 / November 2024
- Published online by Cambridge University Press:
- 11 April 2024, pp. 2859-2912
- Print publication:
- November 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Discriminant and integral basis of number fields defined by exponential Taylor polynomials
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 67 / Issue 2 / May 2024
- Published online by Cambridge University Press:
- 08 April 2024, pp. 528-541
-
- Article
- Export citation
Li coefficients and the quadrilateral zeta function
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 67 / Issue 3 / September 2024
- Published online by Cambridge University Press:
- 08 April 2024, pp. 860-871
- Print publication:
- September 2024
-
- Article
- Export citation
APPROXIMATION OF IRRATIONAL NUMBERS BY PAIRS OF INTEGERS FROM A LARGE SET
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 110 / Issue 3 / December 2024
- Published online by Cambridge University Press:
- 03 April 2024, pp. 439-447
- Print publication:
- December 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Zeros of Rankin–Selberg L-functions in families
- Part of
-
- Journal:
- Compositio Mathematica / Volume 160 / Issue 5 / May 2024
- Published online by Cambridge University Press:
- 03 April 2024, pp. 1041-1072
- Print publication:
- May 2024
-
- Article
- Export citation
NONDEFINABILITY RESULTS FOR ELLIPTIC AND MODULAR FUNCTIONS
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 03 April 2024, pp. 1-20
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Lower Bounds for the Canonical Height of a Unicritical Polynomial and Capacity
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 02 April 2024, e45
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Unit fractions with shifted prime denominators
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 155 / Issue 6 / December 2025
- Published online by Cambridge University Press:
- 02 April 2024, pp. 2285-2295
- Print publication:
- December 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Evaluation of
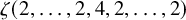 $ \zeta (2,\ldots ,2,4,2,\ldots ,2) $ and period polynomial relations
$ \zeta (2,\ldots ,2,4,2,\ldots ,2) $ and period polynomial relations
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 02 April 2024, e46
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
CHARACTERISATION OF PRIMES DIVIDING THE INDEX OF A CLASS OF POLYNOMIALS AND ITS APPLICATIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 110 / Issue 3 / December 2024
- Published online by Cambridge University Press:
- 01 April 2024, pp. 460-467
- Print publication:
- December 2024
-
- Article
- Export citation
Modular curves and Néron models of generalized Jacobians
- Part of
-
- Journal:
- Compositio Mathematica / Volume 160 / Issue 5 / May 2024
- Published online by Cambridge University Press:
- 26 March 2024, pp. 945-981
- Print publication:
- May 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
THE SUMMED PAPERFOLDING SEQUENCE
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 110 / Issue 2 / October 2024
- Published online by Cambridge University Press:
- 25 March 2024, pp. 189-198
- Print publication:
- October 2024
-
- Article
- Export citation
Omega results for the error term in the square-free divisor problem for square-full integers
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 67 / Issue 4 / December 2024
- Published online by Cambridge University Press:
- 20 March 2024, pp. 1011-1028
- Print publication:
- December 2024
-
- Article
- Export citation
Models and integral differentials of hyperelliptic curves
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 66 / Issue 2 / May 2024
- Published online by Cambridge University Press:
- 18 March 2024, pp. 382-439
- Print publication:
- May 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
L2 to Lp bounds for spectral projectors on the Euclidean two-dimensional torus
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 67 / Issue 2 / May 2024
- Published online by Cambridge University Press:
- 15 March 2024, pp. 431-459
-
- Article
- Export citation
Almost sure convergence of the
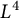 $L^4$ norm of Littlewood polynomials
$L^4$ norm of Littlewood polynomials
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 67 / Issue 3 / September 2024
- Published online by Cambridge University Press:
- 15 March 2024, pp. 872-885
- Print publication:
- September 2024
-
- Article
- Export citation
Geometric structures in pseudo-random graphs
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 77 / Issue 3 / June 2025
- Published online by Cambridge University Press:
- 15 March 2024, pp. 1041-1071
- Print publication:
- June 2025
-
- Article
- Export citation
Discrepancy of rational points in simple algebraic groups
- Part of
-
- Journal:
- Compositio Mathematica / Volume 160 / Issue 4 / April 2024
- Published online by Cambridge University Press:
- 13 March 2024, pp. 836-877
- Print publication:
- April 2024
-
- Article
- Export citation
The sup-norm problem beyond the newform
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 176 / Issue 3 / May 2024
- Published online by Cambridge University Press:
- 12 March 2024, pp. 517-545
- Print publication:
- May 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation