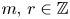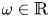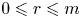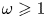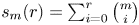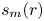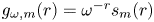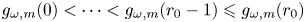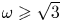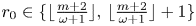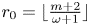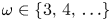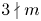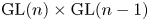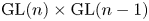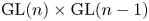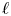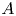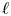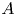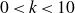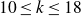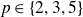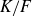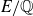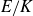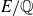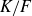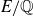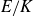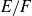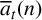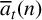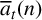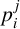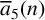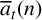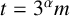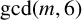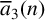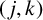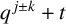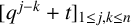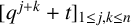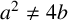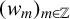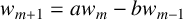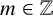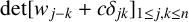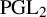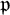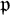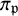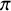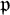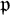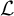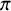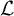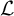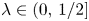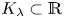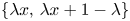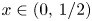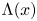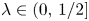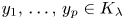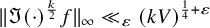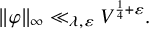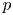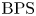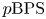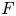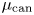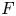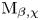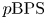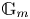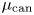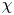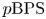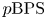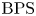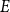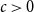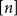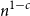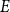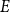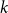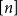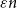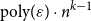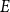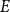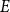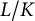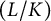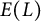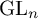Refine listing
Actions for selected content:
2837 results in 11xxx
Maximizing weighted sums of binomial coefficients using generalized continued fractions
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 27 August 2024, pp. 1-16
-
- Article
- Export citation
Period relations for Rankin–Selberg convolutions for
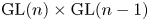 ${\mathrm {GL}}(n)\times {\mathrm {GL}}(n-1)$
${\mathrm {GL}}(n)\times {\mathrm {GL}}(n-1)$
- Part of
-
- Journal:
- Compositio Mathematica / Volume 160 / Issue 8 / August 2024
- Published online by Cambridge University Press:
- 11 September 2024, pp. 1871-1915
- Print publication:
- August 2024
-
- Article
- Export citation
On the integral part of A-motivic cohomology
- Part of
-
- Journal:
- Compositio Mathematica / Volume 160 / Issue 8 / August 2024
- Published online by Cambridge University Press:
- 16 September 2024, pp. 1715-1783
- Print publication:
- August 2024
-
- Article
- Export citation
Differential forms on universal K3 surfaces
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 177 / Issue 1 / July 2024
- Published online by Cambridge University Press:
- 12 July 2024, pp. 1-9
- Print publication:
- July 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Tropical curves in abelian surfaces I: enumeration of curves passing through points
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 177 / Issue 1 / July 2024
- Published online by Cambridge University Press:
- 19 September 2024, pp. 109-148
- Print publication:
- July 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Multiplicative dependence of rational values modulo approximate finitely generated groups
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 177 / Issue 1 / July 2024
- Published online by Cambridge University Press:
- 19 September 2024, pp. 149-165
- Print publication:
- July 2024
-
- Article
- Export citation
The Failure of Galois Descent for p-Selmer Groups of Elliptic Curves
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 177 / Issue 1 / July 2024
- Published online by Cambridge University Press:
- 19 September 2024, pp. 185-218
- Print publication:
- July 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ARITHMETIC PROPERTIES OF AN ANALOGUE OF t-CORE PARTITIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 111 / Issue 1 / February 2025
- Published online by Cambridge University Press:
- 03 June 2024, pp. 68-79
- Print publication:
- February 2025
-
- Article
- Export citation
CHARACTERISTIC POLYNOMIALS OF THE MATRICES WITH
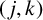 $(\,j,k)$-ENTRY
$(\,j,k)$-ENTRY 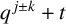 $q^{\,j\pm k}+t$
$q^{\,j\pm k}+t$
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 111 / Issue 2 / April 2025
- Published online by Cambridge University Press:
- 03 June 2024, pp. 228-237
- Print publication:
- April 2025
-
- Article
- Export citation
L-invariants for cohomological representations of PGL(2) over arbitrary number fields
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 30 May 2024, e71
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On a class of self-similar sets which contain finitely many common points
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 30 May 2024, pp. 1-22
-
- Article
- Export citation
Theta functions, fourth moments of eigenforms and the sup-norm problem II
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 12 / 2024
- Published online by Cambridge University Press:
- 30 May 2024, e11
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
BPS invariants from p-adic integrals
- Part of
-
- Journal:
- Compositio Mathematica / Volume 160 / Issue 7 / July 2024
- Published online by Cambridge University Press:
- 30 May 2024, pp. 1525-1550
- Print publication:
- July 2024
-
- Article
- Export citation
A generalisation of Varnavides’s theorem
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 33 / Issue 6 / November 2024
- Published online by Cambridge University Press:
- 29 May 2024, pp. 724-728
-
- Article
- Export citation
Random walks and the “Euclidean” association scheme in finite vector spaces
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 77 / Issue 5 / October 2025
- Published online by Cambridge University Press:
- 24 May 2024, pp. 1664-1685
- Print publication:
- October 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
TWISTED GAN–GROSS–PRASAD CONJECTURE FOR CERTAIN TEMPERED L-PACKETS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 24 / Issue 1 / January 2025
- Published online by Cambridge University Press:
- 24 May 2024, pp. 17-39
- Print publication:
- January 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Counting elements of the congruence subgroup
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 67 / Issue 4 / December 2024
- Published online by Cambridge University Press:
- 22 May 2024, pp. 955-969
- Print publication:
- December 2024
-
- Article
- Export citation
Minimal subfields of elliptic curves
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 67 / Issue 4 / December 2024
- Published online by Cambridge University Press:
- 22 May 2024, pp. 1029-1045
- Print publication:
- December 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ARCHIMEDEAN NEWFORM THEORY FOR
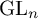 $\operatorname {\mathrm {GL}}_n$
$\operatorname {\mathrm {GL}}_n$
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 24 / Issue 1 / January 2025
- Published online by Cambridge University Press:
- 17 May 2024, pp. 41-116
- Print publication:
- January 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The Heisenberg covering of the Fermat curve
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 77 / Issue 5 / October 2025
- Published online by Cambridge University Press:
- 10 May 2024, pp. 1637-1663
- Print publication:
- October 2025
-
- Article
- Export citation