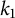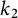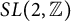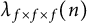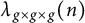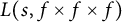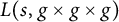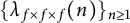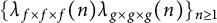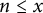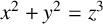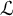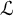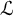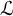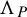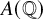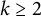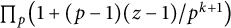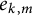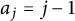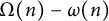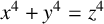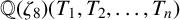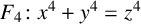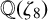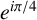Refine listing
Actions for selected content:
2837 results in 11xxx
On the sign changes of Dirichlet coefficients of triple product L-functions
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 67 / Issue 4 / December 2024
- Published online by Cambridge University Press:
- 14 November 2024, pp. 1092-1106
- Print publication:
- December 2024
-
- Article
- Export citation
FROBENIUS NUMBERS ASSOCIATED WITH DIOPHANTINE TRIPLES OF
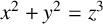 $x^2+y^2=z^3$
$x^2+y^2=z^3$
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 112 / Issue 1 / August 2025
- Published online by Cambridge University Press:
- 14 November 2024, pp. 57-66
- Print publication:
- August 2025
-
- Article
- Export citation
On Greenberg–Benois
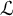 $\mathcal {L}$-invariants and Fontaine–Mazur
$\mathcal {L}$-invariants and Fontaine–Mazur 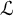 $\mathcal {L}$-invariants
$\mathcal {L}$-invariants
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 67 / Issue 4 / December 2024
- Published online by Cambridge University Press:
- 14 November 2024, pp. 1141-1160
- Print publication:
- December 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Convolution of periodic multiplicative functions and the divisor problem
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 77 / Issue 6 / December 2025
- Published online by Cambridge University Press:
- 14 November 2024, pp. 1966-1984
- Print publication:
- December 2025
-
- Article
- Export citation
Exact dimension functions of the prime continued fraction Cantor set
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 6 / June 2025
- Published online by Cambridge University Press:
- 14 November 2024, pp. 1757-1776
- Print publication:
- June 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ARBITRARILY LARGE p-TORSION IN TATE-SHAFAREVICH GROUPS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 24 / Issue 2 / March 2025
- Published online by Cambridge University Press:
- 12 November 2024, pp. 481-502
- Print publication:
- March 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ON ODA’S PROBLEM AND SPECIAL LOCI
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 24 / Issue 2 / March 2025
- Published online by Cambridge University Press:
- 12 November 2024, pp. 503-539
- Print publication:
- March 2025
-
- Article
- Export citation
TRANSCENDENTAL RUBAN p-ADIC CONTINUED FRACTIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 112 / Issue 1 / August 2025
- Published online by Cambridge University Press:
- 11 November 2024, pp. 80-92
- Print publication:
- August 2025
-
- Article
- Export citation
On elements of prescribed norm in maximal orders of a quaternion algebra
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 77 / Issue 6 / December 2025
- Published online by Cambridge University Press:
- 11 November 2024, pp. 1938-1965
- Print publication:
- December 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Equality cases of the Alexandrov–Fenchel inequality are not in the polynomial hierarchy
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 12 / 2024
- Published online by Cambridge University Press:
- 11 November 2024, e21
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Rational torsion points on abelian surfaces with quaternionic multiplication
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 08 November 2024, e92
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Distribution of the number of prime factors with a given multiplicity
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 67 / Issue 4 / December 2024
- Published online by Cambridge University Press:
- 07 November 2024, pp. 1107-1122
- Print publication:
- December 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
POINTS ON
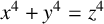 $x^4+y^4=z^4$ OVER QUADRATIC EXTENSIONS OF
$x^4+y^4=z^4$ OVER QUADRATIC EXTENSIONS OF 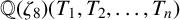 ${\mathbb {Q}}(\zeta _8)(T_1,T_2,\ldots ,T_n)$
${\mathbb {Q}}(\zeta _8)(T_1,T_2,\ldots ,T_n)$
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 111 / Issue 1 / February 2025
- Published online by Cambridge University Press:
- 07 November 2024, pp. 19-31
- Print publication:
- February 2025
-
- Article
- Export citation
Mod p points on shimura varieties of parahoric level
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 12 / 2024
- Published online by Cambridge University Press:
- 06 November 2024, e20
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Intersective sets for sparse sets of integers
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 5 / May 2025
- Published online by Cambridge University Press:
- 06 November 2024, pp. 1370-1402
- Print publication:
- May 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Dimension estimates for badly approximable affine forms
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 5 / May 2025
- Published online by Cambridge University Press:
- 06 November 2024, pp. 1541-1596
- Print publication:
- May 2025
-
- Article
- Export citation
The Brun–Hooley sieve for 𝔽2[X] and squarefree shifts of integer polynomials
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 67 / Issue 4 / November 2024
- Published online by Cambridge University Press:
- 06 November 2024, pp. 1171-1195
-
- Article
- Export citation
On some mod p representations of quaternion algebra over ℚp
- Part of
-
- Journal:
- Compositio Mathematica / Volume 160 / Issue 11 / November 2024
- Published online by Cambridge University Press:
- 03 December 2024, pp. 2585-2655
- Print publication:
- November 2024
-
- Article
- Export citation
Height functions on Hecke orbits and the generalised André–Pink–Zannier conjecture
- Part of
-
- Journal:
- Compositio Mathematica / Volume 160 / Issue 11 / November 2024
- Published online by Cambridge University Press:
- 19 November 2024, pp. 2531-2584
- Print publication:
- November 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Computing the Cassels–Tate pairing for genus two jacobians with rational two-torsion points
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 177 / Issue 3 / November 2024
- Published online by Cambridge University Press:
- 06 December 2024, pp. 415-437
- Print publication:
- November 2024
-
- Article
- Export citation