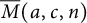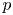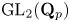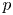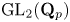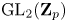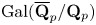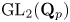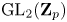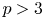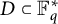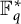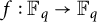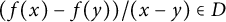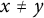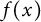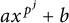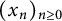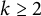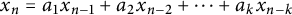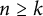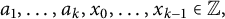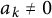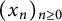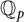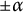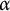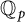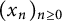Refine listing
Actions for selected content:
2838 results in 11xxx
A function field analog of Jacobi’s theorem on sums of squares and its moments
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 68 / Issue 3 / September 2025
- Published online by Cambridge University Press:
- 10 January 2025, pp. 667-683
- Print publication:
- September 2025
-
- Article
- Export citation
Rarity of pseudo-null Iwasawa modules for p-adic Lie extensions
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 68 / Issue 3 / September 2025
- Published online by Cambridge University Press:
- 10 January 2025, pp. 709-724
- Print publication:
- September 2025
-
- Article
- Export citation
Presentation of an Iwasawa algebra: The pro-p Iwahori of simple, simply connected, split groups
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 68 / Issue 2 / June 2025
- Published online by Cambridge University Press:
- 09 January 2025, pp. 377-394
- Print publication:
- June 2025
-
- Article
- Export citation
Exponential sums over Möbius convolutions with applications to partitions
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 09 January 2025, pp. 1-36
-
- Article
- Export citation
Restricted sumsets in multiplicative subgroups
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 09 January 2025, pp. 1-25
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Asymptotics for crank of overpartitions
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 09 January 2025, pp. 1-34
-
- Article
- Export citation
Effective approximation to complex algebraic numbers by quadratic numbers
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 68 / Issue 1 / March 2025
- Published online by Cambridge University Press:
- 08 January 2025, pp. 262-269
- Print publication:
- March 2025
-
- Article
- Export citation
On the binomial transforms of Apéry-like sequences
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 68 / Issue 2 / June 2025
- Published online by Cambridge University Press:
- 08 January 2025, pp. 359-376
- Print publication:
- June 2025
-
- Article
- Export citation
Restriction of p-adic representations of GL2(Qp) to parahoric subgroups
- Part of
-
- Journal:
- Compositio Mathematica / Volume 161 / Issue 1 / January 2025
- Published online by Cambridge University Press:
- 24 March 2025, pp. 74-119
- Print publication:
- January 2025
-
- Article
- Export citation
Uniformity of quasi-integral points of bounded degree in higher-dimensional orbits
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 178 / Issue 1 / January 2025
- Published online by Cambridge University Press:
- 08 January 2025, pp. 15-29
- Print publication:
- January 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Chai's conjecture for semiabelian Jacobians
- Part of
-
- Journal:
- Compositio Mathematica / Volume 161 / Issue 1 / January 2025
- Published online by Cambridge University Press:
- 24 March 2025, pp. 120-147
- Print publication:
- January 2025
-
- Article
- Export citation
Zero-full law for well approximable sets in missing digit sets
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 178 / Issue 1 / January 2025
- Published online by Cambridge University Press:
- 20 February 2025, pp. 81-102
- Print publication:
- January 2025
-
- Article
- Export citation
Full Poissonian local statistics of slowly growing sequences
- Part of
-
- Journal:
- Compositio Mathematica / Volume 161 / Issue 1 / January 2025
- Published online by Cambridge University Press:
- 24 March 2025, pp. 148-180
- Print publication:
- January 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A NOTE ON THE LARGE SIEVE INEQUALITY FOR MODULI GENERATED BY A QUADRATIC
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 112 / Issue 2 / October 2025
- Published online by Cambridge University Press:
- 26 December 2024, pp. 254-259
- Print publication:
- October 2025
-
- Article
- Export citation
A Szemerédi type theorem for sets of positive density in approximate lattices
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 7 / July 2025
- Published online by Cambridge University Press:
- 23 December 2024, pp. 2023-2053
- Print publication:
- July 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A classification of Shimura curves in
 $ \mathscr {A}_g$
$ \mathscr {A}_g$
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 20 December 2024, pp. 1-27
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Bilinear Kloosterman sums in function fields and the distribution of irreducible polynomials
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 20 December 2024, pp. 1-26
-
- Article
- Export citation
A strengthening of McConnel’s theorem on permutations over finite fields
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 68 / Issue 1 / March 2025
- Published online by Cambridge University Press:
- 20 December 2024, pp. 213-218
- Print publication:
- March 2025
-
- Article
- Export citation
p-Adic quotient sets: Linear recurrence sequences with reducible characteristic polynomials
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 68 / Issue 1 / March 2025
- Published online by Cambridge University Press:
- 11 December 2024, pp. 177-186
- Print publication:
- March 2025
-
- Article
- Export citation
Some inequalities between
 $M(a,b,c;L;n)$ and the partition function
$M(a,b,c;L;n)$ and the partition function  $p(n)$
$p(n)$
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 77 / Issue 6 / December 2025
- Published online by Cambridge University Press:
- 10 December 2024, pp. 2148-2170
- Print publication:
- December 2025
-
- Article
- Export citation