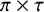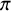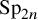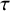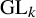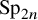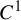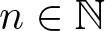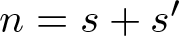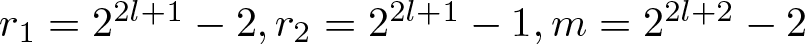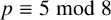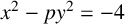Refine listing
Actions for selected content:
2838 results in 11xxx
THE COHOMOLOGY OF p-ADIC DELIGNE-LUSZTIG SCHEMES OF COXETER TYPE
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 24 / Issue 4 / July 2025
- Published online by Cambridge University Press:
- 10 February 2025, pp. 1429-1462
- Print publication:
- July 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Mean values of multiplicative functions and applications to residue-class distribution
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 68 / Issue 3 / August 2025
- Published online by Cambridge University Press:
- 10 February 2025, pp. 712-730
-
- Article
- Export citation
An efficient asymmetric removal lemma and its limitations
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 10 February 2025, e38
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ON GALOIS GROUPS OF POWER COMPOSITIONAL NONIC POLYNOMIALS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 112 / Issue 3 / December 2025
- Published online by Cambridge University Press:
- 10 February 2025, pp. 458-472
- Print publication:
- December 2025
-
- Article
- Export citation
IRRATIONALITY OF ZEROS OF POLYGAMMA FUNCTIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 112 / Issue 3 / December 2025
- Published online by Cambridge University Press:
- 10 February 2025, pp. 430-440
- Print publication:
- December 2025
-
- Article
- Export citation
Doubling constructions and tensor product L-functions: coverings of the symplectic group
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 10 February 2025, e27
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
CORRECTION TO ‘ADDITIVE AND SUBTRACTIVE BASES OF
 $ \mathbb {Z}_m$ IN AVERAGE’
$ \mathbb {Z}_m$ IN AVERAGE’
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 111 / Issue 3 / June 2025
- Published online by Cambridge University Press:
- 10 February 2025, pp. 566-567
- Print publication:
- June 2025
-
- Article
- Export citation
RANK 2
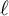 $\ell $-ADIC LOCAL SYSTEMS AND HIGGS BUNDLES OVER A CURVE
$\ell $-ADIC LOCAL SYSTEMS AND HIGGS BUNDLES OVER A CURVE
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 24 / Issue 3 / May 2025
- Published online by Cambridge University Press:
- 10 February 2025, pp. 891-960
- Print publication:
- May 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Dynamical Diophantine approximation and shrinking targets for
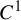 $C^{1}$ weakly conformal IFSs with overlaps
$C^{1}$ weakly conformal IFSs with overlaps
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 6 / June 2025
- Published online by Cambridge University Press:
- 10 February 2025, pp. 1777-1826
- Print publication:
- June 2025
-
- Article
- Export citation
A bound on the
 $\mu $-invariants of supersingular elliptic curves
$\mu $-invariants of supersingular elliptic curves
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 68 / Issue 3 / September 2025
- Published online by Cambridge University Press:
- 07 February 2025, pp. 787-796
- Print publication:
- September 2025
-
- Article
- Export citation
AN ANALOGUE OF AN IDENTITY OF JACOBI
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 112 / Issue 3 / December 2025
- Published online by Cambridge University Press:
- 07 February 2025, pp. 528-535
- Print publication:
- December 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On the L-polynomials of curves over finite fields
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 06 February 2025, pp. 1-49
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
DIGITALLY RESTRICTED SETS AND THE GOLDBACH CONJECTURE
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 111 / Issue 3 / June 2025
- Published online by Cambridge University Press:
- 04 February 2025, pp. 469-477
- Print publication:
- June 2025
-
- Article
- Export citation
ON PSEUDO-NULLITY OF THE FINE MORDELL–WEIL GROUP
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 112 / Issue 1 / August 2025
- Published online by Cambridge University Press:
- 03 February 2025, pp. 71-79
- Print publication:
- August 2025
-
- Article
- Export citation
On the structure of non-negative integer sets which have identical representation functions
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 68 / Issue 2 / May 2025
- Published online by Cambridge University Press:
- 03 February 2025, pp. 655-674
-
- Article
- Export citation
PARITY BIAS IN FUNDAMENTAL UNITS OF REAL QUADRATIC FIELDS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 112 / Issue 1 / August 2025
- Published online by Cambridge University Press:
- 03 February 2025, pp. 67-70
- Print publication:
- August 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Furstenberg systems of pretentious and MRT multiplicative functions
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 9 / September 2025
- Published online by Cambridge University Press:
- 03 February 2025, pp. 2765-2844
- Print publication:
- September 2025
-
- Article
- Export citation
Local newforms for generic representations of unramified even unitary groups I: Even conductor case
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 03 February 2025, e23
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On the linear AFL: the non-basic case
- Part of
-
- Journal:
- Compositio Mathematica / Volume 161 / Issue 2 / February 2025
- Published online by Cambridge University Press:
- 23 June 2025, pp. 385-425
- Print publication:
- February 2025
-
- Article
- Export citation
Waring’s problem with restricted digits
- Part of
-
- Journal:
- Compositio Mathematica / Volume 161 / Issue 2 / February 2025
- Published online by Cambridge University Press:
- 24 June 2025, pp. 341-364
- Print publication:
- February 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation