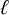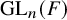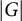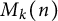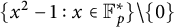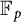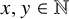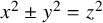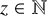Refine listing
Actions for selected content:
2838 results in 11xxx
Kodaira–Spencer isomorphisms and degeneracy maps on Iwahori-level Hilbert modular varieties: the saving trace
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 28 February 2025, e50
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Theory of heat equations for sigma functions
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 67 / Issue 3 / September 2025
- Published online by Cambridge University Press:
- 28 February 2025, pp. 365-422
- Print publication:
- September 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
NOTE ON A DYNAMICAL GENERALISATION OF THE PRIME NUMBER THEOREM FOR ARITHMETIC PROGRESSIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society , First View
- Published online by Cambridge University Press:
- 27 February 2025, pp. 1-8
-
- Article
- Export citation
ARITHMETIC-GEOMETRIC MEAN SEQUENCES OVER FINITE FIELDS
 $\mathbb {F}_q$, WHERE
$\mathbb {F}_q$, WHERE  $q\equiv 5$ (mod 8)
$q\equiv 5$ (mod 8)
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 112 / Issue 3 / December 2025
- Published online by Cambridge University Press:
- 27 February 2025, pp. 473-484
- Print publication:
- December 2025
-
- Article
- Export citation
Hilbert’s 10th problem via Mordell curves
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 68 / Issue 3 / September 2025
- Published online by Cambridge University Press:
- 26 February 2025, pp. 939-949
- Print publication:
- September 2025
-
- Article
- Export citation
POLYNOMIALS REPRESENTED BY NORM FORMS VIA THE BETA SIEVE
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 24 / Issue 4 / July 2025
- Published online by Cambridge University Press:
- 25 February 2025, pp. 1463-1519
- Print publication:
- July 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On the
 $\mu$-invariant of two-variable
$\mu$-invariant of two-variable  $2$-adic
$2$-adic  $\boldsymbol{L}$-functions
$\boldsymbol{L}$-functions
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 67 / Issue 3 / September 2025
- Published online by Cambridge University Press:
- 24 February 2025, pp. 325-355
- Print publication:
- September 2025
-
- Article
- Export citation
Asymptotics and sign patterns of Hecke polynomial coefficients
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 68 / Issue 3 / September 2025
- Published online by Cambridge University Press:
- 21 February 2025, pp. 914-926
- Print publication:
- September 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The Ramanujan and Sato–Tate Conjectures for Bianchi modular forms
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 13 / 2025
- Published online by Cambridge University Press:
- 21 February 2025, e10
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Cuspidal
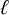 ${\ell }$-modular representations of
${\ell }$-modular representations of 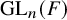 $\operatorname {GL}_n({ F})$ distinguished by a Galois involution
$\operatorname {GL}_n({ F})$ distinguished by a Galois involution
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 20 February 2025, e48
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Multiplicative structure of shifted multiplicative subgroups and its applications to Diophantine tuples
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 19 February 2025, pp. 1-41
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On local Galois deformation rings: generalised tori
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 18 February 2025, e45
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ON MALLE’S CONJECTURE FOR THE PRODUCT OF SYMMETRIC AND NILPOTENT GROUPS
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 259 / September 2025
- Published online by Cambridge University Press:
- 17 February 2025, pp. 473-498
- Print publication:
- September 2025
-
- Article
- Export citation
A NOTE ON CHARACTER SUMS OVER SHORT MOVING INTERVALS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 24 / Issue 4 / July 2025
- Published online by Cambridge University Press:
- 13 February 2025, pp. 1395-1427
- Print publication:
- July 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Partition regularity of Pythagorean pairs
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 13 / 2025
- Published online by Cambridge University Press:
- 12 February 2025, e5
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Reduction of bielliptic surfaces
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 68 / Issue 3 / September 2025
- Published online by Cambridge University Press:
- 12 February 2025, pp. 856-873
- Print publication:
- September 2025
-
- Article
- Export citation
EXISTENCE OF K-MULTIMAGIC SQUARES AND MAGIC SQUARES OF kth POWERS WITH DISTINCT ENTRIES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 112 / Issue 3 / December 2025
- Published online by Cambridge University Press:
- 11 February 2025, pp. 441-448
- Print publication:
- December 2025
-
- Article
- Export citation
ON NEW MINIMAL EXCLUDANTS OF OVERPARTITIONS RELATED TO SOME q-SERIES OF RAMANUJAN
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 112 / Issue 1 / August 2025
- Published online by Cambridge University Press:
- 11 February 2025, pp. 1-13
- Print publication:
- August 2025
-
- Article
- Export citation
ON MINIMAL ADDITIVE COMPLEMENTS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 112 / Issue 3 / December 2025
- Published online by Cambridge University Press:
- 11 February 2025, pp. 410-417
- Print publication:
- December 2025
-
- Article
- Export citation
Average Analytic Ranks of Elliptic Curves over Number Fields
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 11 February 2025, e40
-
- Article
-
- You have access
- Open access
- HTML
- Export citation