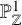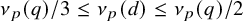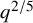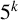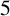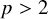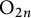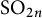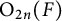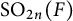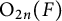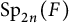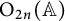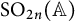Refine listing
Actions for selected content:
2838 results in 11xxx
Squarefree values of polynomial discriminants II
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 13 / 2025
- Published online by Cambridge University Press:
- 13 May 2025, e17
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Almost sure upper bound for a model problem for multiplicative chaos in number theory
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 179 / Issue 1 / July 2025
- Published online by Cambridge University Press:
- 13 May 2025, pp. 29-44
- Print publication:
- July 2025
-
- Article
- Export citation
On inhomogeneous Poissonian pair correlations
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 179 / Issue 1 / July 2025
- Published online by Cambridge University Press:
- 13 May 2025, pp. 17-27
- Print publication:
- July 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The global Gan-Gross-Prasad conjecture for unitary groups. II. From Eisenstein series to Bessel periods
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 13 / 2025
- Published online by Cambridge University Press:
- 13 May 2025, e16
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
MONOGENITY OF THE COMPOSITION OF POLYNOMIALS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society , First View
- Published online by Cambridge University Press:
- 08 May 2025, pp. 1-9
-
- Article
- Export citation
A REMARK ON GENERALISED CUBIC PARTITIONS MODULO
 $5$
$5$
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society , First View
- Published online by Cambridge University Press:
- 07 May 2025, pp. 1-5
-
- Article
- Export citation
FONCTIONS ADDITIVES EN BASE DE CANTOR LE LONG DES NOMBRES PREMIERS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 24 / Issue 5 / September 2025
- Published online by Cambridge University Press:
- 06 May 2025, pp. 1807-1865
- Print publication:
- September 2025
-
- Article
- Export citation
Asymptotic second moment of Dirichlet L-functions along a thin coset
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 02 May 2025, e83
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
THE WZ METHOD AND FLAWLESS WZ PAIRS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society , First View
- Published online by Cambridge University Press:
- 28 April 2025, pp. 1-9
-
- Article
- Export citation
Multiplicative dependence in linear recurrence sequences
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 68 / Issue 4 / December 2025
- Published online by Cambridge University Press:
- 21 April 2025, pp. 1278-1288
- Print publication:
- December 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A note on the values of Mahler measure in quadratic fields
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 68 / Issue 4 / December 2025
- Published online by Cambridge University Press:
- 21 April 2025, pp. 1267-1277
- Print publication:
- December 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Quasi-polynomial representations of double affine Hecke algebras
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 16 April 2025, e73
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ON
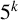 $5^k$-REGULAR PARTITIONS MODULO POWERS OF
$5^k$-REGULAR PARTITIONS MODULO POWERS OF 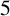 $5$
$5$
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 112 / Issue 3 / December 2025
- Published online by Cambridge University Press:
- 14 April 2025, pp. 449-457
- Print publication:
- December 2025
-
- Article
- Export citation
 $ \epsilon $-ISOMORPHISMS FOR RANK ONE
$ \epsilon $-ISOMORPHISMS FOR RANK ONE  $( \varphi , \Gamma )$-MODULES OVER LUBIN-TATE ROBBA RINGS
$( \varphi , \Gamma )$-MODULES OVER LUBIN-TATE ROBBA RINGS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 24 / Issue 5 / September 2025
- Published online by Cambridge University Press:
- 11 April 2025, pp. 1895-1994
- Print publication:
- September 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
COMBINATORIAL PROOFS FOR TWO-COLOUR PARTITIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society , First View
- Published online by Cambridge University Press:
- 11 April 2025, pp. 1-5
-
- Article
- Export citation
Canonical integral models for Shimura varieties of abelian type
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 07 April 2025, e69
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The local converse theorem for quasi-split
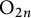 $\mathrm {O}_{2n}$ and
$\mathrm {O}_{2n}$ and 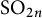 $\mathrm {SO}_{2n}$
$\mathrm {SO}_{2n}$
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 07 April 2025, pp. 1-38
-
- Article
- Export citation
Bounds on the Pythagoras number and indecomposables in biquadratic fields
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 68 / Issue 3 / August 2025
- Published online by Cambridge University Press:
- 31 March 2025, pp. 843-868
-
- Article
- Export citation
Ordinary isogeny graphs with level structure
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 68 / Issue 4 / December 2025
- Published online by Cambridge University Press:
- 27 March 2025, pp. 1144-1162
- Print publication:
- December 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Iterating additive polynomials over finite fields
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 68 / Issue 3 / August 2025
- Published online by Cambridge University Press:
- 25 March 2025, pp. 795-810
-
- Article
- Export citation