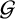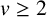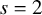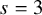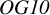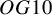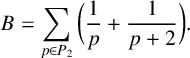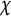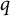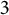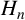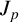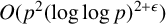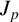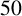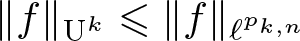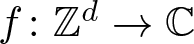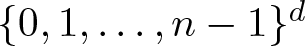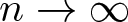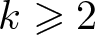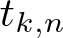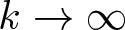Refine listing
Actions for selected content:
2838 results in 11xxx
EISENSTEIN COHOMOLOGY FOR ORTHOGONAL GROUPS AND THE SPECIAL VALUES OF L-FUNCTIONS FOR
 $\mathrm {GL}_1 \times \mathrm {O}(2n)$
$\mathrm {GL}_1 \times \mathrm {O}(2n)$
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 24 / Issue 6 / November 2025
- Published online by Cambridge University Press:
- 28 July 2025, pp. 2463-2522
- Print publication:
- November 2025
-
- Article
- Export citation
Hook length inequalities for t-regular partitions in the t-aspect
- Part of
-
- Journal:
- Canadian Mathematical Bulletin , First View
- Published online by Cambridge University Press:
- 24 July 2025, pp. 1-12
-
- Article
- Export citation
DIMENSIONS OF SETS AVOIDING APPROXIMATE NONTRIVIAL ZEROS OF LINEAR PATTERNS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society , First View
- Published online by Cambridge University Press:
- 21 July 2025, pp. 1-12
-
- Article
- Export citation
RIGID INNER FORMS OVER GLOBAL FUNCTION FIELDS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 24 / Issue 6 / November 2025
- Published online by Cambridge University Press:
- 21 July 2025, pp. 2181-2256
- Print publication:
- November 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Semi-stable and splitting models for unitary Shimura varieties over ramified places. I.
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 17 July 2025, e119
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On the Fitting ideals of anticyclotomic Selmer groups of elliptic curves with good ordinary reduction
- Part of
-
- Journal:
- Canadian Mathematical Bulletin , First View
- Published online by Cambridge University Press:
- 14 July 2025, pp. 1-11
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On a theorem of Mattila in the finite p-adic setting
- Part of
-
- Journal:
- Canadian Mathematical Bulletin , First View
- Published online by Cambridge University Press:
- 14 July 2025, pp. 1-15
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Finite groups of symplectic birational transformations of IHS manifolds of
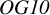 $\mathit {OG10}$ type
$\mathit {OG10}$ type
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 14 July 2025, e117
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Elliptic curves and spin
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 179 / Issue 3 / November 2025
- Published online by Cambridge University Press:
- 11 July 2025, pp. 519-539
- Print publication:
- November 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Modularity of arithmetic special divisors for unitary Shimura varieties (with an appendix by Yujie Xu)
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 10 July 2025, e111
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
IMPROVED UPPER BOUND ON BRUN’S CONSTANT UNDER GRH
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society , First View
- Published online by Cambridge University Press:
- 04 July 2025, pp. 1-11
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Moments, Exponential Sums, and Monodromy Groups
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 26 June 2025, e101
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On off-diagonal Ramsey numbers for vector spaces over
 $\mathbb{F}_{2}$
$\mathbb{F}_{2}$
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 179 / Issue 2 / September 2025
- Published online by Cambridge University Press:
- 25 June 2025, pp. 503-518
- Print publication:
- September 2025
-
- Article
- Export citation
On the
 $\mathfrak{M}_H(G)$-property
$\mathfrak{M}_H(G)$-property
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 179 / Issue 2 / September 2025
- Published online by Cambridge University Press:
- 24 June 2025, pp. 449-501
- Print publication:
- September 2025
-
- Article
- Export citation
Opposing average congruence class biases in the cyclicity and Koblitz conjectures for elliptic curves
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 24 June 2025, pp. 1-51
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Functional Transcendence of Periods and the Geometric André–Grothendieck Period Conjecture
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 23 June 2025, e97
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On L-values of elliptic curves twisted by cubic Dirichlet characters
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 20 June 2025, pp. 1-25
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ON ESWARATHASAN–LEVINE AND BOYD’S CONJECTURES FOR HARMONIC NUMBERS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society , First View
- Published online by Cambridge University Press:
- 20 June 2025, pp. 1-11
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Congruences modulo powers of 5 for partition k-tuples with 5-cores
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 68 / Issue 4 / November 2025
- Published online by Cambridge University Press:
- 17 June 2025, pp. 1245-1261
-
- Article
- Export citation
Sharp estimates for Gowers norms on discrete cubes
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 16 June 2025, pp. 1-27
-
- Article
- Export citation