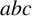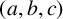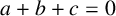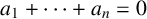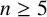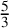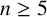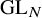Refine listing
Actions for selected content:
2838 results in 11xxx
On Dirichlet non-improvable numbers and shrinking target problems
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 11 / November 2025
- Published online by Cambridge University Press:
- 11 June 2025, pp. 3540-3568
- Print publication:
- November 2025
-
- Article
- Export citation
 $B_h$-sets of real and complex numbers
$B_h$-sets of real and complex numbers
- Part of
-
- Journal:
- Canadian Mathematical Bulletin , First View
- Published online by Cambridge University Press:
- 11 June 2025, pp. 1-5
-
- Article
- Export citation
Class groups and Selmer groups in special families
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 68 / Issue 4 / December 2025
- Published online by Cambridge University Press:
- 10 June 2025, pp. 1315-1337
- Print publication:
- December 2025
-
- Article
- Export citation
IMPROVED LOWER BOUNDS FOR STRONG n-CONJECTURES
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 119 / Issue 1 / August 2025
- Published online by Cambridge University Press:
- 02 June 2025, pp. 61-81
- Print publication:
- August 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Revisiting Dwork cohomology: visibility and divisibility of Frobenius eigenvalues in rigid cohomology
- Part of
-
- Journal:
- Compositio Mathematica / Volume 161 / Issue 6 / June 2025
- Published online by Cambridge University Press:
- 01 September 2025, pp. 1215-1249
- Print publication:
- June 2025
-
- Article
-
- You have access
- HTML
- Export citation
Functional degrees and arithmetic applications III: beyond prime exponent
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 179 / Issue 2 / September 2025
- Published online by Cambridge University Press:
- 30 May 2025, pp. 409-438
- Print publication:
- September 2025
-
- Article
- Export citation
Congruent elliptic curves and the
 $\tau $-component in the Iwasawa main conjecture
$\tau $-component in the Iwasawa main conjecture
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 179 / Issue 2 / September 2025
- Published online by Cambridge University Press:
- 29 May 2025, pp. 373-408
- Print publication:
- September 2025
-
- Article
- Export citation
A criterion for the simple normality of fractional powers of two via the Riemann zeta function
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 29 May 2025, pp. 1-24
-
- Article
- Export citation
Weighted sieves with switching
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 179 / Issue 2 / September 2025
- Published online by Cambridge University Press:
- 28 May 2025, pp. 351-372
- Print publication:
- September 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Euler Products at the Centre and Applications to Chebyshev’s Bias
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 179 / Issue 2 / September 2025
- Published online by Cambridge University Press:
- 27 May 2025, pp. 331-349
- Print publication:
- September 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The p-adic limits of class numbers in
 ${\mathbb{Z}}_p$-towers
${\mathbb{Z}}_p$-towers
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 179 / Issue 2 / September 2025
- Published online by Cambridge University Press:
- 23 May 2025, pp. 299-329
- Print publication:
- September 2025
-
- Article
- Export citation
An analogue of the Milnor conjecture for the de Rham-Witt complex in characteristic 2
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 22 May 2025, e87
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Eisenstein Cohomology for
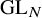 $\mathrm {GL}_N$ and the special values of Rankin–Selberg L-functions over a totally imaginary number field
$\mathrm {GL}_N$ and the special values of Rankin–Selberg L-functions over a totally imaginary number field
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 22 May 2025, e86
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
DIFFRACTION OF THE PRIMES AND OTHER SETS OF ZERO DENSITY
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 119 / Issue 2 / October 2025
- Published online by Cambridge University Press:
- 21 May 2025, pp. 202-245
- Print publication:
- October 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
POSITIVE DENSITY FOR CONSECUTIVE RUNS OF SUMS OF TWO SQUARES
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 24 / Issue 5 / September 2025
- Published online by Cambridge University Press:
- 21 May 2025, pp. 1995-2046
- Print publication:
- September 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The Chowla conjecture and Landau–Siegel zeroes
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 179 / Issue 1 / July 2025
- Published online by Cambridge University Press:
- 19 May 2025, pp. 167-187
- Print publication:
- July 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Annihilating class groups in p-elementary abelian extensions
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 179 / Issue 1 / July 2025
- Published online by Cambridge University Press:
- 19 May 2025, pp. 145-166
- Print publication:
- July 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
SQUARE-FULL VALUES OF QUADRATIC POLYNOMIALS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society , First View
- Published online by Cambridge University Press:
- 16 May 2025, pp. 1-15
-
- Article
- Export citation
MONOTONIC COLLATZ SUBSEQUENCES WITH TERMS CONGRUENT MODULO A FIXED POWER OF TWO
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 112 / Issue 3 / December 2025
- Published online by Cambridge University Press:
- 16 May 2025, pp. 418-429
- Print publication:
- December 2025
-
- Article
- Export citation
Uniform sets with few progressions via colourings
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 179 / Issue 1 / July 2025
- Published online by Cambridge University Press:
- 15 May 2025, pp. 79-103
- Print publication:
- July 2025
-
- Article
- Export citation