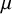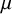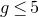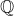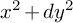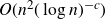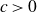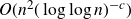Refine listing
Actions for selected content:
2838 results in 11xxx
Symmetric multiple zeta functions
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 24 March 2025, pp. 1-35
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Shifted moments of quadratic Dirichlet L-functions
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 68 / Issue 4 / December 2025
- Published online by Cambridge University Press:
- 24 March 2025, pp. 1116-1143
- Print publication:
- December 2025
-
- Article
- Export citation
Deformation theory for prismatic G-displays
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 21 March 2025, e61
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
TWO NEW TRUNCATED IDENTITIES AND PARTITION THEOREMS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society , First View
- Published online by Cambridge University Press:
- 21 March 2025, pp. 1-8
-
- Article
- Export citation
ON SOME EFFECTIVE RESULTS INVOLVING ZEROS OF THE RIEMANN ZETA FUNCTION
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 111 / Issue 3 / June 2025
- Published online by Cambridge University Press:
- 21 March 2025, pp. 563-565
- Print publication:
- June 2025
-
- Article
-
- You have access
- HTML
- Export citation
Rationality and arithmetic of the moduli of abelian varieties
- Part of
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
COVERING INTEGERS BY
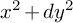 $x^2 + dy^2$
$x^2 + dy^2$
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 24 / Issue 3 / May 2025
- Published online by Cambridge University Press:
- 18 March 2025, pp. 847-889
- Print publication:
- May 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
BINARY AND TERNARY CONGRUENCES INVOLVING INTERVALS AND SETS MODULO A PRIME
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 112 / Issue 2 / October 2025
- Published online by Cambridge University Press:
- 18 March 2025, pp. 237-247
- Print publication:
- October 2025
-
- Article
- Export citation
NOMBRE DE PETITS POINTS SUR UNE VARIÉTÉ ABÉLIENNE
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 24 / Issue 3 / May 2025
- Published online by Cambridge University Press:
- 18 March 2025, pp. 705-761
- Print publication:
- May 2025
-
- Article
- Export citation
SIMPLE TYPE THEORY FOR METAPLECTIC COVERS OF
 $\operatorname {GL}(r)$ OVER A NON-ARCHIMEDEAN LOCAL FIELD
$\operatorname {GL}(r)$ OVER A NON-ARCHIMEDEAN LOCAL FIELD
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 24 / Issue 4 / July 2025
- Published online by Cambridge University Press:
- 18 March 2025, pp. 1263-1335
- Print publication:
- July 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Deformations of Theta Integrals and A Conjecture of Gross-Zagier
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 14 March 2025, e54
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Arthur packets for pure real forms of symplectic and special orthogonal groups
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 68 / Issue 4 / December 2025
- Published online by Cambridge University Press:
- 12 March 2025, pp. 1047-1068
- Print publication:
- December 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
MAILLET’S PROPERTY AND MAHLER’S CONJECTURE ON LIOUVILLE NUMBERS FAIL FOR MATRICES
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 119 / Issue 1 / August 2025
- Published online by Cambridge University Press:
- 10 March 2025, pp. 106-127
- Print publication:
- August 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A linear AFL for quaternion algebras
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 04 March 2025, pp. 1-23
-
- Article
- Export citation
Semisimple random walks on the torus
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 10 / October 2025
- Published online by Cambridge University Press:
- 03 March 2025, pp. 3090-3147
- Print publication:
- October 2025
-
- Article
- Export citation
Improved bounds for skew corner-free sets
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 178 / Issue 2 / March 2025
- Published online by Cambridge University Press:
- 04 April 2025, pp. 177-192
- Print publication:
- March 2025
-
- Article
- Export citation
Geometric local systems on the projective line minus four points
- Part of
-
- Journal:
- Compositio Mathematica / Volume 161 / Issue 3 / March 2025
- Published online by Cambridge University Press:
- 01 July 2025, pp. 536-554
- Print publication:
- March 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Overconvergence of étale
 $(\varphi,\Gamma)$-modules in families
$(\varphi,\Gamma)$-modules in families
- Part of
-
- Journal:
- Compositio Mathematica / Volume 161 / Issue 3 / March 2025
- Published online by Cambridge University Press:
- 10 July 2025, pp. 555-593
- Print publication:
- March 2025
-
- Article
- Export citation
The sum-product problem for integers with few prime factors
- Part of
-
- Journal:
- Compositio Mathematica / Volume 161 / Issue 3 / March 2025
- Published online by Cambridge University Press:
- 26 June 2025, pp. 427-446
- Print publication:
- March 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A non-flag arithmetic regularity lemma and counting lemma
- Part of
-
- Journal:
- Compositio Mathematica / Volume 161 / Issue 3 / March 2025
- Published online by Cambridge University Press:
- 02 July 2025, pp. 635-679
- Print publication:
- March 2025
-
- Article
- Export citation