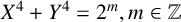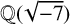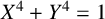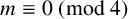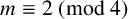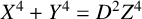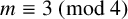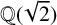Refine listing
Actions for selected content:
2838 results in 11xxx
Unimodular Hunting II
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 26 August 2025, e136
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Murmurations of modular forms and p-power coefficients
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 180 / Issue 1 / January 2026
- Published online by Cambridge University Press:
- 26 August 2025, pp. 65-92
- Print publication:
- January 2026
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
2-Elongated plane partitions and powers of 7: the localization method applied to a genus 1 congruence family
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 22 August 2025, pp. 1-43
-
- Article
- Export citation
Cancellation in sums over special sequences on
 $\mathrm {GL}_m$ and their applications
$\mathrm {GL}_m$ and their applications
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 20 August 2025, pp. 1-30
-
- Article
- Export citation
THE FERMAT QUARTIC X4 + Y4 = 2m IN QUADRATIC NUMBER FIELDS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society , First View
- Published online by Cambridge University Press:
- 15 August 2025, pp. 1-10
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Oscillation results for the summatory functions of fake
 $\mu $’s
$\mu $’s
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 15 August 2025, pp. 1-44
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Limit theorems for a class of unbounded observables with an application to ‘Sampling the Lindelöf hypothesis’
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 46 / Issue 1 / January 2026
- Published online by Cambridge University Press:
- 12 August 2025, pp. 34-92
- Print publication:
- January 2026
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Metallic mean Wang tiles I: self-similarity, aperiodicity and minimality
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 12 August 2025, e133
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Moments of random multiplicative functions over function fields
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 179 / Issue 3 / November 2025
- Published online by Cambridge University Press:
- 08 August 2025, pp. 785-819
- Print publication:
- November 2025
-
- Article
- Export citation
Counting cyclic extensions with local conditions and applications to L-values in the critical strip
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 08 August 2025, pp. 1-39
-
- Article
- Export citation
Mean values of arithmetic functions and application to sums of powers
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 180 / Issue 1 / January 2026
- Published online by Cambridge University Press:
- 08 August 2025, pp. 1-13
- Print publication:
- January 2026
-
- Article
- Export citation
On congruence subgroups generated by two parabolic rational matrices
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 180 / Issue 1 / January 2026
- Published online by Cambridge University Press:
- 08 August 2025, pp. 15-34
- Print publication:
- January 2026
-
- Article
- Export citation
Ergodicity and algebraicity of the fast and slow triangle maps
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 46 / Issue 1 / January 2026
- Published online by Cambridge University Press:
- 08 August 2025, pp. 93-127
- Print publication:
- January 2026
-
- Article
- Export citation
Bianchi modular forms and the rationality of periods
- Part of
-
- Journal:
- Canadian Mathematical Bulletin , First View
- Published online by Cambridge University Press:
- 07 August 2025, pp. 1-19
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Number of solutions to a special type of unit equations in two unknowns, III
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 179 / Issue 3 / November 2025
- Published online by Cambridge University Press:
- 07 August 2025, pp. 737-784
- Print publication:
- November 2025
-
- Article
- Export citation
Infinitely repeated partitions of Liouville numbers
- Part of
-
- Journal:
- Canadian Mathematical Bulletin , First View
- Published online by Cambridge University Press:
- 06 August 2025, pp. 1-8
-
- Article
- Export citation
Arithmetic Transfer for inner forms of
 $GL_{2n}$
$GL_{2n}$
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 04 August 2025, e128
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Smooth numbers in arithmetic progressions to large moduli
- Part of
-
- Journal:
- Compositio Mathematica / Volume 161 / Issue 8 / August 2025
- Published online by Cambridge University Press:
- 12 September 2025, pp. 1923-1974
- Print publication:
- August 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Characterising local fields of positive characteristic by Galois theory and the Brauer group
- Part of
-
- Journal:
- Compositio Mathematica / Volume 161 / Issue 8 / August 2025
- Published online by Cambridge University Press:
- 13 October 2025, pp. 2136-2153
- Print publication:
- August 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
AN ASYMPTOTIC ESTIMATE FOR THE CHARACTERISTIC AND NUMBER OF FIXED POINTS OF THE RIEMANN ZETA FUNCTION
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 260 / December 2025
- Published online by Cambridge University Press:
- 01 August 2025, pp. 648-665
- Print publication:
- December 2025
-
- Article
- Export citation