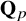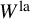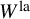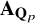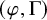Refine listing
Actions for selected content:
2838 results in 11xxx
ON THE DESCENT CONJECTURE FOR RATIONAL POINTS AND ZERO-CYCLES
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu , First View
- Published online by Cambridge University Press:
- 19 November 2025, pp. 1-49
-
- Article
- Export citation
An asymptotic formula for Tate–Shafarevich groups of CM elliptic curves at supersingular primes
- Part of
-
- Journal:
- Canadian Mathematical Bulletin , First View
- Published online by Cambridge University Press:
- 13 November 2025, pp. 1-15
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Signature maps from positive cones on algebras with involution
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 12 November 2025, pp. 1-26
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
NON-DIOPHANTINE SETS IN RINGS OF FUNCTIONS
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 12 November 2025, pp. 1-14
-
- Article
- Export citation
ON ADDITIVE COMPLEMENTS IN THE COMPLEMENT OF A SET OF NATURAL NUMBERS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society , First View
- Published online by Cambridge University Press:
- 07 November 2025, pp. 1-13
-
- Article
- Export citation
On the Hilbert space derived from the Weil distribution
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 03 November 2025, pp. 1-24
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On The Schinzel–Wójcik Problem Under Hypothesis H
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society , First View
- Published online by Cambridge University Press:
- 03 November 2025, pp. 1-13
-
- Article
- Export citation
ON THE LARGEST PRIME DIVISOR OF n! + 1
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society , First View
- Published online by Cambridge University Press:
- 03 November 2025, pp. 1-14
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The structure of Lonely Runner spectra
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society , First View
- Published online by Cambridge University Press:
- 24 October 2025, pp. 1-19
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
NON-SEMI-STABLE LOCI IN HECKE STACKS AND FARGUES’ CONJECTURE
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu , First View
- Published online by Cambridge University Press:
- 23 October 2025, pp. 1-31
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Inequality arising from the iterated Laguerre operator for various partitions
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society , First View
- Published online by Cambridge University Press:
- 23 October 2025, pp. 1-22
-
- Article
- Export citation
Local aspects of the Sidorenko property for linear equations
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 23 October 2025, e177
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Higher power sums of Fourier coefficients of symmetric square L-functions
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society , First View
- Published online by Cambridge University Press:
- 21 October 2025, pp. 1-22
-
- Article
- Export citation
A classification of
 $\mathbb {Q}$-linear maps from
$\mathbb {Q}$-linear maps from  $\overline {\mathbb {Q}}^\times /\overline {\mathbb {Q}}^\times _{\mathrm {tors}}$ to
$\overline {\mathbb {Q}}^\times /\overline {\mathbb {Q}}^\times _{\mathrm {tors}}$ to  $\mathbb {R}$
$\mathbb {R}$
- Part of
-
- Journal:
- Canadian Mathematical Bulletin , First View
- Published online by Cambridge University Press:
- 21 October 2025, pp. 1-19
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
THE NUMBER OF PARTS IN A RANDOM t-REGULAR PARTITION
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society , First View
- Published online by Cambridge University Press:
- 16 October 2025, pp. 1-15
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The dual pair
 $\mathrm {Aut}(C)\times F_{4}$ (p-adic case)
$\mathrm {Aut}(C)\times F_{4}$ (p-adic case)
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 16 October 2025, e174
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ON INTEGRAL LOCAL SHIMURA VARIETIES
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu , First View
- Published online by Cambridge University Press:
- 14 October 2025, pp. 1-69
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Locally analytic vectors and decompletion in mixed characteristic
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 14 October 2025, e173
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Revisiting sums and products in countable and finite fields
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems , First View
- Published online by Cambridge University Press:
- 13 October 2025, pp. 1-32
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
AN EFFECTIVE VERSION OF THE PRIMITIVE ELEMENT THEOREM
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society , First View
- Published online by Cambridge University Press:
- 13 October 2025, pp. 1-8
-
- Article
- Export citation





 .
.