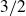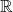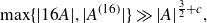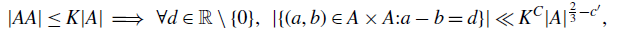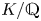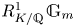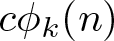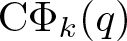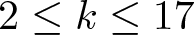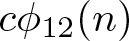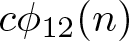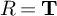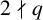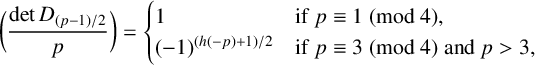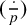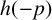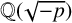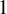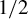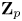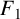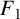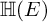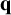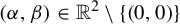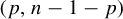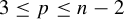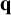Refine listing
Actions for selected content:
2837 results in 11xxx
A better than
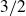 $3/2$ exponent for iterated sums and products over
$3/2$ exponent for iterated sums and products over 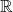 $\mathbb R$
$\mathbb R$
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 177 / Issue 1 / July 2024
- Published online by Cambridge University Press:
- 10 May 2024, pp. 11-22
- Print publication:
- July 2024
-
- Article
- Export citation
A solution to the Erdős–Sárközy–Sós problem on asymptotic Sidon bases of order 3
- Part of
-
- Journal:
- Compositio Mathematica / Volume 160 / Issue 6 / June 2024
- Published online by Cambridge University Press:
- 10 May 2024, pp. 1418-1432
- Print publication:
- June 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
NORMAL BASES FOR FUNCTION FIELDS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 110 / Issue 1 / August 2024
- Published online by Cambridge University Press:
- 06 May 2024, pp. 44-55
- Print publication:
- August 2024
-
- Article
- Export citation
Weak approximation on the norm one torus
- Part of
-
- Journal:
- Compositio Mathematica / Volume 160 / Issue 6 / June 2024
- Published online by Cambridge University Press:
- 06 May 2024, pp. 1304-1348
- Print publication:
- June 2024
-
- Article
- Export citation
BOUNDS FOR MOMENTS OF QUADRATIC DIRICHLET CHARACTER SUMS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 111 / Issue 1 / February 2025
- Published online by Cambridge University Press:
- 06 May 2024, pp. 43-47
- Print publication:
- February 2025
-
- Article
- Export citation
Spectral decomposition of genuine cusp forms over global function fields
- Part of
-
- Journal:
- Compositio Mathematica / Volume 160 / Issue 6 / June 2024
- Published online by Cambridge University Press:
- 06 May 2024, pp. 1194-1260
- Print publication:
- June 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Some congruences for 12-coloured generalized Frobenius partitions
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 67 / Issue 3 / August 2024
- Published online by Cambridge University Press:
- 02 May 2024, pp. 778-793
-
- Article
- Export citation
Poissonian pair correlation for directions in multi-dimensional affine lattices and escape of mass estimates for embedded horospheres
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 1 / January 2025
- Published online by Cambridge University Press:
- 26 April 2024, pp. 218-246
- Print publication:
- January 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
WILES DEFECT OF HECKE ALGEBRAS VIA LOCAL-GLOBAL ARGUMENTS: WITH AN APPENDIX BY NAJMUDDIN FAKHRUDDIN AND CHANDRASHEKHAR B. KHARE
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 23 / Issue 6 / November 2024
- Published online by Cambridge University Press:
- 25 April 2024, pp. 2461-2541
- Print publication:
- November 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ON MATRICES ARISING IN FINITE FIELD HYPERGEOMETRIC FUNCTIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 110 / Issue 3 / December 2024
- Published online by Cambridge University Press:
- 22 April 2024, pp. 421-426
- Print publication:
- December 2024
-
- Article
- Export citation
ON GENERALISED LEGENDRE MATRICES INVOLVING ROOTS OF UNITY OVER FINITE FIELDS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 110 / Issue 2 / October 2024
- Published online by Cambridge University Press:
- 22 April 2024, pp. 199-210
- Print publication:
- October 2024
-
- Article
- Export citation
Schmidt games and Cantor winning sets
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 1 / January 2025
- Published online by Cambridge University Press:
- 19 April 2024, pp. 71-110
- Print publication:
- January 2025
-
- Article
- Export citation
Attractors are not algebraic
- Part of
-
- Journal:
- Compositio Mathematica / Volume 160 / Issue 5 / May 2024
- Published online by Cambridge University Press:
- 18 April 2024, pp. 1073-1100
- Print publication:
- May 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ASYMPTOTIC BEHAVIOUR FOR PRODUCTS OF CONSECUTIVE PARTIAL QUOTIENTS IN CONTINUED FRACTIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 110 / Issue 3 / December 2024
- Published online by Cambridge University Press:
- 18 April 2024, pp. 448-459
- Print publication:
- December 2024
-
- Article
- Export citation
Completed prismatic F-crystals and crystalline Zp-local systems
- Part of
-
- Journal:
- Compositio Mathematica / Volume 160 / Issue 5 / May 2024
- Published online by Cambridge University Press:
- 18 April 2024, pp. 1101-1166
- Print publication:
- May 2024
-
- Article
- Export citation
NEW CONGRUENCES FOR THE TRUNCATED APPELL SERIES
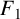 $F_1$
$F_1$
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 111 / Issue 1 / February 2025
- Published online by Cambridge University Press:
- 18 April 2024, pp. 146-153
- Print publication:
- February 2025
-
- Article
- Export citation
ON THE DISTINCTION OF IWAHORI-SPHERICAL DISCRETE SERIES REPRESENTATIONS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 24 / Issue 1 / January 2025
- Published online by Cambridge University Press:
- 17 April 2024, pp. 1-15
- Print publication:
- January 2025
-
- Article
- Export citation
Asymptotic distribution for pairs of linear and quadratic forms at integral vectors
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 1 / January 2025
- Published online by Cambridge University Press:
- 17 April 2024, pp. 111-139
- Print publication:
- January 2025
-
- Article
- Export citation
KOBAYASHI-OCHIAI’S FINITENESS THEOREM FOR ORBIFOLD PAIRS OF GENERAL TYPE
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 23 / Issue 6 / November 2024
- Published online by Cambridge University Press:
- 17 April 2024, pp. 2713-2732
- Print publication:
- November 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Affine Bruhat order and Demazure products
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 15 April 2024, e53
-
- Article
-
- You have access
- Open access
- HTML
- Export citation