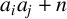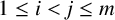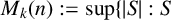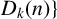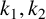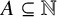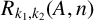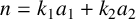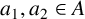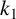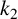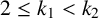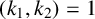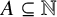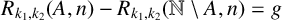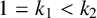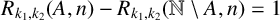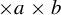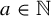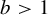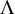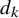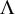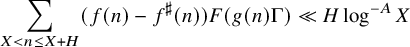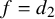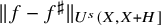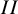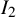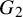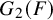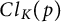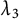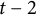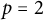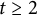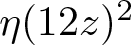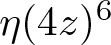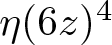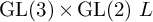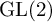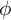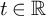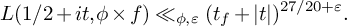Refine listing
Actions for selected content:
2837 results in 11xxx
The tamely ramified geometric quantitative minimal ramification problem
- Part of
-
- Journal:
- Compositio Mathematica / Volume 160 / Issue 1 / January 2024
- Published online by Cambridge University Press:
- 09 November 2023, pp. 21-51
- Print publication:
- January 2024
-
- Article
- Export citation
Tropical invariants for binary quintics and reduction types of Picard curves
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 66 / Issue 1 / January 2024
- Published online by Cambridge University Press:
- 06 November 2023, pp. 65-87
- Print publication:
- January 2024
-
- Article
- Export citation
AN EFFECTIVE BOUND FOR GENERALISED DIOPHANTINE m-TUPLES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 109 / Issue 2 / April 2024
- Published online by Cambridge University Press:
- 06 November 2023, pp. 242-253
- Print publication:
- April 2024
-
- Article
- Export citation
Eisenstein congruences among Euler systems
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 67 / Issue 2 / June 2024
- Published online by Cambridge University Press:
- 06 November 2023, pp. 425-446
- Print publication:
- June 2024
-
- Article
- Export citation
A new way to tackle a conjecture of Rémond
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 76 / Issue 6 / December 2024
- Published online by Cambridge University Press:
- 31 October 2023, pp. 2049-2072
- Print publication:
- December 2024
-
- Article
- Export citation
Smooth integers and de Bruijn's approximation Ʌ
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 155 / Issue 3 / June 2025
- Published online by Cambridge University Press:
- 31 October 2023, pp. 792-820
- Print publication:
- June 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
PARTITIONS OF NATURAL NUMBERS AND THEIR WEIGHTED REPRESENTATION FUNCTIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 110 / Issue 1 / August 2024
- Published online by Cambridge University Press:
- 27 October 2023, pp. 12-18
- Print publication:
- August 2024
-
- Article
- Export citation
Autocorrelations of characteristic polynomials for the Alternative Circular Unitary Ensemble
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 66 / Issue 1 / January 2024
- Published online by Cambridge University Press:
- 27 October 2023, pp. 51-64
- Print publication:
- January 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On local Galois deformation rings
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 11 / 2023
- Published online by Cambridge University Press:
- 26 October 2023, e30
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
LINEAR INDEPENDENCE OF VALUES OF THE q-EXPONENTIAL AND RELATED FUNCTIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 109 / Issue 3 / June 2024
- Published online by Cambridge University Press:
- 23 October 2023, pp. 453-463
- Print publication:
- June 2024
-
- Article
- Export citation
Some measure rigidity and equidistribution results for β-maps
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 9 / September 2024
- Published online by Cambridge University Press:
- 23 October 2023, pp. 2581-2598
- Print publication:
- September 2024
-
- Article
- Export citation
ON THE EXCEPTIONAL SET OF TRANSCENDENTAL ENTIRE FUNCTIONS IN SEVERAL VARIABLES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 110 / Issue 1 / August 2024
- Published online by Cambridge University Press:
- 20 October 2023, pp. 64-71
- Print publication:
- August 2024
-
- Article
- Export citation
Bounded cohomology is not a profinite invariant
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 67 / Issue 2 / June 2024
- Published online by Cambridge University Press:
- 20 October 2023, pp. 379-390
- Print publication:
- June 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Isogeny graphs on superspecial abelian varieties: eigenvalues and connection to Bruhat–Tits buildings
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 76 / Issue 6 / December 2024
- Published online by Cambridge University Press:
- 20 October 2023, pp. 1891-1916
- Print publication:
- December 2024
-
- Article
- Export citation
Higher uniformity of arithmetic functions in short intervals I. All intervals
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 11 / 2023
- Published online by Cambridge University Press:
- 19 October 2023, e29
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The Local Langlands Conjecture for
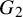 $G_2$
$G_2$
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 11 / 2023
- Published online by Cambridge University Press:
- 19 October 2023, e28
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Infinite families of Artin–Schreier function fields with any prescribed class group rank
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 76 / Issue 5 / October 2024
- Published online by Cambridge University Press:
- 19 October 2023, pp. 1773-1794
- Print publication:
- October 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Representatives of similarity classes of matrices over PIDs corresponding to ideal classes
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 66 / Issue 1 / January 2024
- Published online by Cambridge University Press:
- 18 October 2023, pp. 88-103
- Print publication:
- January 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On the vanishing of the coefficients of CM eta quotients
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 66 / Issue 4 / November 2023
- Published online by Cambridge University Press:
- 18 October 2023, pp. 1202-1216
-
- Article
- Export citation
UNIFORM BOUNDS FOR
 $\operatorname {GL}(3)\times \operatorname {GL}(2)$ L-FUNCTIONS
$\operatorname {GL}(3)\times \operatorname {GL}(2)$ L-FUNCTIONS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 23 / Issue 4 / July 2024
- Published online by Cambridge University Press:
- 17 October 2023, pp. 1607-1650
- Print publication:
- July 2024
-
- Article
- Export citation