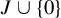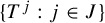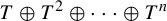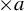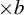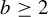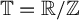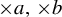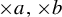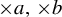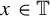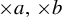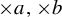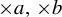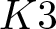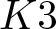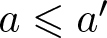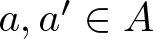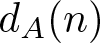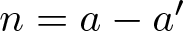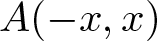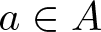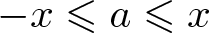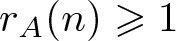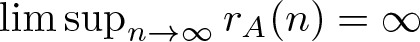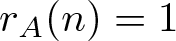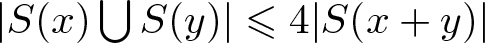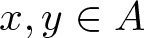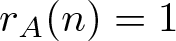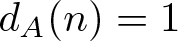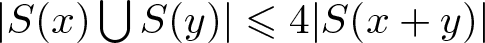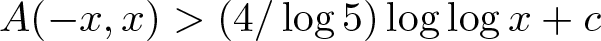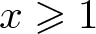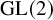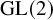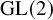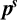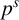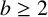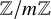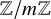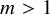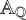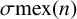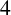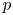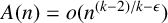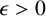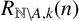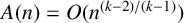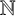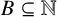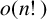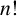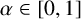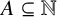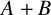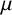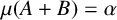Refine listing
Actions for selected content:
2838 results in 11xxx
Disjoint hypercyclicity, Sidon sets and weakly mixing operators
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 5 / May 2024
- Published online by Cambridge University Press:
- 22 August 2023, pp. 1315-1329
- Print publication:
- May 2024
-
- Article
- Export citation
Connected components of affine Deligne–Lusztig varieties for unramified groups
- Part of
-
- Journal:
- Compositio Mathematica / Volume 159 / Issue 10 / October 2023
- Published online by Cambridge University Press:
- 17 August 2023, pp. 2051-2088
- Print publication:
- October 2023
-
- Article
- Export citation
Weil Sums over Small Subgroups
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 176 / Issue 1 / January 2024
- Published online by Cambridge University Press:
- 15 August 2023, pp. 39-53
- Print publication:
- January 2024
-
- Article
- Export citation
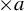 $\times a$ and
$\times a$ and 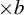 $\times b$ empirical measures, the irregular set and entropy
$\times b$ empirical measures, the irregular set and entropy
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 6 / June 2024
- Published online by Cambridge University Press:
- 15 August 2023, pp. 1673-1692
- Print publication:
- June 2024
-
- Article
- Export citation
Exact formulae and Turán inequalities for Vafa–Witten invariants of
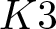 $K3$ surfaces
$K3$ surfaces
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 66 / Issue 3 / August 2023
- Published online by Cambridge University Press:
- 08 August 2023, pp. 845-861
-
- Article
- Export citation
Every Salem number is a difference of two Pisot numbers
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 66 / Issue 3 / August 2023
- Published online by Cambridge University Press:
- 08 August 2023, pp. 862-867
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On the density of bounded bases
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 66 / Issue 3 / August 2023
- Published online by Cambridge University Press:
- 07 August 2023, pp. 832-844
-
- Article
- Export citation
Exotic Monoidal Structures and Abstractly Automorphic Representations for
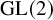 $\mathrm {GL}(2)$
$\mathrm {GL}(2)$
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 11 / 2023
- Published online by Cambridge University Press:
- 03 August 2023, e20
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
GHOSTS AND CONGRUENCES FOR
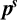 $\boldsymbol {p}^{\boldsymbol {s}}$-APPROXIMATIONS OF HYPERGEOMETRIC PERIODS
$\boldsymbol {p}^{\boldsymbol {s}}$-APPROXIMATIONS OF HYPERGEOMETRIC PERIODS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 116 / Issue 1 / February 2024
- Published online by Cambridge University Press:
- 02 August 2023, pp. 96-127
- Print publication:
- February 2024
-
- Article
- Export citation
EVERY ARITHMETIC PROGRESSION CONTAINS INFINITELY MANY b-NIVEN NUMBERS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 109 / Issue 3 / June 2024
- Published online by Cambridge University Press:
- 31 July 2023, pp. 409-413
- Print publication:
- June 2024
-
- Article
- Export citation
SUM OF VALUES OF THE IDEAL CLASS ZETA-FUNCTION OVER NONTRIVIAL ZEROS OF THE RIEMANN ZETA-FUNCTION
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 109 / Issue 2 / April 2024
- Published online by Cambridge University Press:
- 31 July 2023, pp. 288-300
- Print publication:
- April 2024
-
- Article
- Export citation
Twisted GGP problems and conjectures
- Part of
-
- Journal:
- Compositio Mathematica / Volume 159 / Issue 9 / September 2023
- Published online by Cambridge University Press:
- 31 July 2023, pp. 1916-1973
- Print publication:
- September 2023
-
- Article
- Export citation
Decidability of the class of all the rings
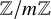 $\mathbb {Z}/m\mathbb {Z}$: A problem of Ax
$\mathbb {Z}/m\mathbb {Z}$: A problem of Ax
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 24 July 2023, e64
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ON A CONJECTURE FOR A REFINEMENT OF THE SUM OF MINIMAL EXCLUDANTS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 109 / Issue 2 / April 2024
- Published online by Cambridge University Press:
- 20 July 2023, pp. 276-287
- Print publication:
- April 2024
-
- Article
- Export citation
Equivalent criterion for the grand Riemann hypothesis associated with Maass cusp forms
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 154 / Issue 5 / October 2024
- Published online by Cambridge University Press:
- 19 July 2023, pp. 1348-1363
- Print publication:
- October 2024
-
- Article
- Export citation
G-valued crystalline deformation rings in the Fontaine–Laffaille range
- Part of
-
- Journal:
- Compositio Mathematica / Volume 159 / Issue 8 / August 2023
- Published online by Cambridge University Press:
- 17 July 2023, pp. 1791-1832
- Print publication:
- August 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ON MONOTONE INCREASING REPRESENTATION FUNCTIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 109 / Issue 2 / April 2024
- Published online by Cambridge University Press:
- 17 July 2023, pp. 196-205
- Print publication:
- April 2024
-
- Article
- Export citation
SELF-DIVISIBLE ULTRAFILTERS AND CONGRUENCES IN
 $\beta {\mathbb {Z}}$
$\beta {\mathbb {Z}}$
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 90 / Issue 3 / September 2025
- Published online by Cambridge University Press:
- 17 July 2023, pp. 1180-1197
- Print publication:
- September 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ON THE DENSITY OF SUMSETS, II
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 109 / Issue 3 / June 2024
- Published online by Cambridge University Press:
- 17 July 2023, pp. 414-419
- Print publication:
- June 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
SHORT CHARACTER SUMS AND THEIR APPLICATIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 108 / Issue 2 / October 2023
- Published online by Cambridge University Press:
- 11 July 2023, pp. 339-340
- Print publication:
- October 2023
-
- Article
-
- You have access
- HTML
- Export citation