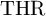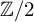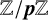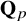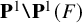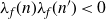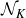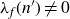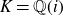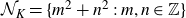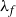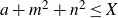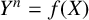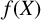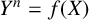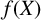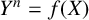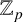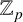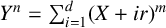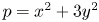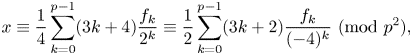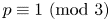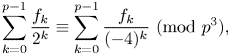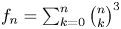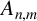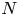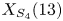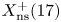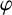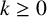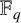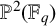Refine listing
Actions for selected content:
2838 results in 11xxx
REAL TOPOLOGICAL HOCHSCHILD HOMOLOGY OF SCHEMES
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 23 / Issue 3 / May 2024
- Published online by Cambridge University Press:
- 07 June 2023, pp. 1461-1518
- Print publication:
- May 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Around Exponential-Algebraic Closedness
- Part of
-
- Journal:
- Bulletin of Symbolic Logic / Volume 29 / Issue 2 / June 2023
- Published online by Cambridge University Press:
- 18 July 2023, p. 300
- Print publication:
- June 2023
-
- Article
-
- You have access
- Export citation
RANK JUMPS AND GROWTH OF SHAFAREVICH–TATE GROUPS FOR ELLIPTIC CURVES IN
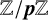 ${\mathbb {Z}}/\boldsymbol{p}{\mathbb {Z}}$-EXTENSIONS
${\mathbb {Z}}/\boldsymbol{p}{\mathbb {Z}}$-EXTENSIONS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 116 / Issue 1 / February 2024
- Published online by Cambridge University Press:
- 29 May 2023, pp. 1-38
- Print publication:
- February 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Riesz-type criteria for L-functions in the Selberg class
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 76 / Issue 3 / June 2024
- Published online by Cambridge University Press:
- 29 May 2023, pp. 1062-1088
- Print publication:
- June 2024
-
- Article
- Export citation
Factorisation de la cohomologie étale p-adique de la tour de Drinfeld
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 11 / 2023
- Published online by Cambridge University Press:
- 26 May 2023, e16
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The first-order theory of binary overlap-free words is decidable
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 76 / Issue 4 / August 2024
- Published online by Cambridge University Press:
- 26 May 2023, pp. 1144-1162
- Print publication:
- August 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
From the Ideal Theorem to the class number
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 4 / December 2023
- Published online by Cambridge University Press:
- 26 May 2023, pp. 1368-1375
- Print publication:
- December 2023
-
- Article
- Export citation
Sign changes of fourier coefficients of holomorphic cusp forms at norm form arguments
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 175 / Issue 3 / November 2023
- Published online by Cambridge University Press:
- 23 May 2023, pp. 539-567
- Print publication:
- November 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
p-adic Eichler–Shimura maps for the modular curve
- Part of
-
- Journal:
- Compositio Mathematica / Volume 159 / Issue 6 / June 2023
- Published online by Cambridge University Press:
- 22 May 2023, pp. 1214-1249
- Print publication:
- June 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Distribution and moments of the error term in the lattice point counting problem for three-dimensional Cygan–Korányi balls
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 154 / Issue 3 / June 2024
- Published online by Cambridge University Press:
- 19 May 2023, pp. 830-861
- Print publication:
- June 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
DIOPHANTINE EQUATIONS OF THE FORM
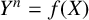 $Y^n=f(X)$ OVER FUNCTION FIELDS
$Y^n=f(X)$ OVER FUNCTION FIELDS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 108 / Issue 3 / December 2023
- Published online by Cambridge University Press:
- 18 May 2023, pp. 379-390
- Print publication:
- December 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On two congruence conjectures of Z.-W. Sun involving Franel numbers
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 154 / Issue 3 / June 2024
- Published online by Cambridge University Press:
- 16 May 2023, pp. 887-905
- Print publication:
- June 2024
-
- Article
- Export citation
An energy decomposition theorem for matrices and related questions
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 4 / December 2023
- Published online by Cambridge University Press:
- 15 May 2023, pp. 1280-1295
- Print publication:
- December 2023
-
- Article
- Export citation
ON THE DIVISIBILITY OF SUMS OF q-SUPER CATALAN NUMBERS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 109 / Issue 2 / April 2024
- Published online by Cambridge University Press:
- 15 May 2023, pp. 215-224
- Print publication:
- April 2024
-
- Article
- Export citation
Quadratic Chabauty for modular curves: algorithms and examples
- Part of
-
- Journal:
- Compositio Mathematica / Volume 159 / Issue 6 / June 2023
- Published online by Cambridge University Press:
- 15 May 2023, pp. 1111-1152
- Print publication:
- June 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ON THE ITERATES OF THE SHIFTED EULER’S FUNCTION
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 109 / Issue 2 / April 2024
- Published online by Cambridge University Press:
- 12 May 2023, pp. 206-214
- Print publication:
- April 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Equidistribution for matings of quadratic maps with the modular group
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 3 / March 2024
- Published online by Cambridge University Press:
- 12 May 2023, pp. 859-887
- Print publication:
- March 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
TANGENT-FILLING PLANE CURVES OVER FINITE FIELDS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 109 / Issue 2 / April 2024
- Published online by Cambridge University Press:
- 02 May 2023, pp. 301-315
- Print publication:
- April 2024
-
- Article
- Export citation
Zariski dense orbits for regular self-maps of split semiabelian varieties in positive characteristic
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 175 / Issue 3 / November 2023
- Published online by Cambridge University Press:
- 02 May 2023, pp. 479-519
- Print publication:
- November 2023
-
- Article
- Export citation
On the derived category of the Iwahori–Hecke algebra
- Part of
-
- Journal:
- Compositio Mathematica / Volume 159 / Issue 5 / May 2023
- Published online by Cambridge University Press:
- 04 May 2023, pp. 1042-1110
- Print publication:
- May 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation