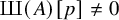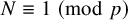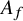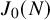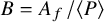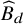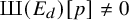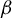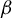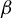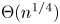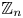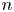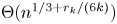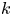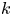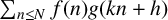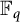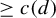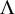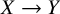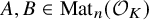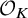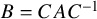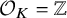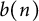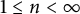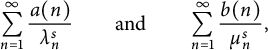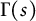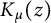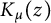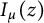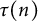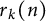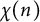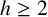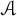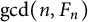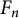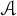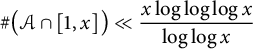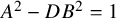Refine listing
Actions for selected content:
2812 results in 11xxx
Elements of prime order in Tate–Shafarevich groups of abelian varieties over
 ${\mathbb Q}$
${\mathbb Q}$
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 10 / 2022
- Published online by Cambridge University Press:
- 04 November 2022, e98
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The natural extension of the random beta-transformation
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 43 / Issue 11 / November 2023
- Published online by Cambridge University Press:
- 04 November 2022, pp. 3861-3896
- Print publication:
- November 2023
-
- Article
- Export citation
Brownian bridge expansions for Lévy area approximations and particular values of the Riemann zeta function
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 32 / Issue 3 / May 2023
- Published online by Cambridge University Press:
- 03 November 2022, pp. 370-397
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Discrepancy in modular arithmetic progressions
- Part of
-
- Journal:
- Compositio Mathematica / Volume 158 / Issue 11 / November 2022
- Published online by Cambridge University Press:
- 01 December 2022, pp. 2082-2108
- Print publication:
- November 2022
-
- Article
- Export citation
On the distribution of rational points on ramified covers of abelian varieties
- Part of
-
- Journal:
- Compositio Mathematica / Volume 158 / Issue 11 / November 2022
- Published online by Cambridge University Press:
- 07 December 2022, pp. 2109-2155
- Print publication:
- November 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Smooth hypersurfaces in abelian varieties over arithmetic rings
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 10 / 2022
- Published online by Cambridge University Press:
- 28 October 2022, e97
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
AFFINE CONVOLUTIONS, RAMANUJAN–FOURIER EXPANSIONS AND SOPHIE GERMAIN PRIMES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 108 / Issue 1 / August 2023
- Published online by Cambridge University Press:
- 25 October 2022, pp. 11-18
- Print publication:
- August 2023
-
- Article
- Export citation
On a conjecture of M. R. Murty and V. K. Murty
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 2 / June 2023
- Published online by Cambridge University Press:
- 25 October 2022, pp. 679-681
- Print publication:
- June 2023
-
- Article
- Export citation
GOOD REDUCTION AND CYCLIC COVERS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 23 / Issue 1 / January 2024
- Published online by Cambridge University Press:
- 24 October 2022, pp. 463-494
- Print publication:
- January 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Nearly sharp Lang–Weil bounds for a hypersurface
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 2 / June 2023
- Published online by Cambridge University Press:
- 18 October 2022, pp. 654-664
- Print publication:
- June 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Periodic expansion of one by Salem numbers
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 43 / Issue 9 / September 2023
- Published online by Cambridge University Press:
- 14 October 2022, pp. 2841-2862
- Print publication:
- September 2023
-
- Article
- Export citation
Computation of lattice isomorphisms and the integral matrix similarity problem
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 10 / 2022
- Published online by Cambridge University Press:
- 10 October 2022, e87
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
An improvement on Schmidt’s bound on the number of number fields of bounded discriminant and small degree
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 10 / 2022
- Published online by Cambridge University Press:
- 10 October 2022, e86
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Benford behavior and distribution in residue classes of large prime factors
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 2 / June 2023
- Published online by Cambridge University Press:
- 10 October 2022, pp. 626-642
- Print publication:
- June 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Two general series identities involving modified Bessel functions and a class of arithmetical functions
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 75 / Issue 6 / December 2023
- Published online by Cambridge University Press:
- 10 October 2022, pp. 1800-1830
- Print publication:
- December 2023
-
- Article
- Export citation
ON MINIMAL RESTRICTED ASYMPTOTIC BASES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 107 / Issue 3 / June 2023
- Published online by Cambridge University Press:
- 06 October 2022, pp. 368-373
- Print publication:
- June 2023
-
- Article
- Export citation
ZAREMBA, SALEM AND THE FRACTAL NATURE OF GHOST DISTRIBUTIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 107 / Issue 3 / June 2023
- Published online by Cambridge University Press:
- 06 October 2022, pp. 374-389
- Print publication:
- June 2023
-
- Article
- Export citation
On the greatest common divisor of n and the nth Fibonacci number, II
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 2 / June 2023
- Published online by Cambridge University Press:
- 06 October 2022, pp. 617-625
- Print publication:
- June 2023
-
- Article
- Export citation
Polynomials over structured grids
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 32 / Issue 2 / March 2023
- Published online by Cambridge University Press:
- 04 October 2022, pp. 284-298
-
- Article
- Export citation
Betti maps, Pell equations in polynomials and almost-Belyi maps
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 10 / 2022
- Published online by Cambridge University Press:
- 04 October 2022, e84
-
- Article
-
- You have access
- Open access
- HTML
- Export citation