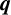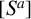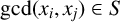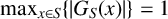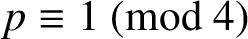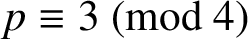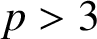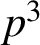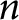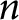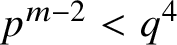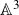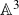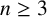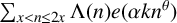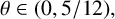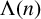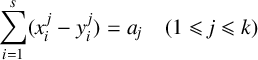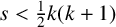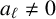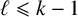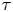Refine listing
Actions for selected content:
2812 results in 11xxx
A NEW
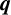 $\boldsymbol {q}$-ANALOGUE OF VAN HAMME’S (A.2) SUPERCONGRUENCE
$\boldsymbol {q}$-ANALOGUE OF VAN HAMME’S (A.2) SUPERCONGRUENCE
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 107 / Issue 1 / February 2023
- Published online by Cambridge University Press:
- 20 May 2022, pp. 22-30
- Print publication:
- February 2023
-
- Article
- Export citation
ON THE DIVISIBILITY AMONG POWER LCM MATRICES ON GCD-CLOSED SETS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 107 / Issue 1 / February 2023
- Published online by Cambridge University Press:
- 19 May 2022, pp. 31-39
- Print publication:
- February 2023
-
- Article
- Export citation
NEW GENERALISATIONS OF VAN HAMME’S (G.2) SUPERCONGRUENCE
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 107 / Issue 2 / April 2023
- Published online by Cambridge University Press:
- 18 May 2022, pp. 177-183
- Print publication:
- April 2023
-
- Article
- Export citation
Hensel minimality I
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 10 / 2022
- Published online by Cambridge University Press:
- 16 May 2022, e11
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Limiting Betti distributions of Hilbert schemes on n points
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 1 / March 2023
- Published online by Cambridge University Press:
- 13 May 2022, pp. 243-258
- Print publication:
- March 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Random symmetric matrices: rank distribution and irreducibility of the characteristic polynomial
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 174 / Issue 2 / March 2023
- Published online by Cambridge University Press:
- 12 May 2022, pp. 233-246
- Print publication:
- March 2023
-
- Article
- Export citation
Bounds for spectral projectors on tori
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 10 / 2022
- Published online by Cambridge University Press:
- 12 May 2022, e24
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On the structure of spectral and tiling subsets of cyclic groups
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 10 / 2022
- Published online by Cambridge University Press:
- 10 May 2022, e23
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Casting light on shadow Somos sequences
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 65 / Issue S1 / May 2023
- Published online by Cambridge University Press:
- 10 May 2022, pp. S87-S101
- Print publication:
- May 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Number fields without universal quadratic forms of small rank exist in most degrees
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 174 / Issue 2 / March 2023
- Published online by Cambridge University Press:
- 06 May 2022, pp. 225-231
- Print publication:
- March 2023
-
- Article
- Export citation
Higher rank motivic Donaldson–Thomas invariants of
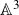 $\mathbb A^3$ via wall-crossing, and asymptotics
$\mathbb A^3$ via wall-crossing, and asymptotics
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 174 / Issue 1 / January 2023
- Published online by Cambridge University Press:
- 05 May 2022, pp. 97-122
- Print publication:
- January 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Torsion points on isogenous abelian varieties
- Part of
-
- Journal:
- Compositio Mathematica / Volume 158 / Issue 5 / May 2022
- Published online by Cambridge University Press:
- 20 July 2022, pp. 1020-1051
- Print publication:
- May 2022
-
- Article
- Export citation
PRIMITIVE ELEMENT PAIRS WITH A PRESCRIBED TRACE IN THE CUBIC EXTENSION OF A FINITE FIELD
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 106 / Issue 3 / December 2022
- Published online by Cambridge University Press:
- 25 April 2022, pp. 458-462
- Print publication:
- December 2022
-
- Article
- Export citation
AVERAGES OF EXPONENTIAL TWISTS OF THE VON MANGOLDT FUNCTION
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 106 / Issue 3 / December 2022
- Published online by Cambridge University Press:
- 25 April 2022, pp. 425-430
- Print publication:
- December 2022
-
- Article
- Export citation
Effective rigid analytic trivializations for Drinfeld modules
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 75 / Issue 3 / June 2023
- Published online by Cambridge University Press:
- 20 April 2022, pp. 713-742
- Print publication:
- June 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ON THE INHOMOGENEOUS VINOGRADOV SYSTEM
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 106 / Issue 3 / December 2022
- Published online by Cambridge University Press:
- 19 April 2022, pp. 396-403
- Print publication:
- December 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ON FINE SELMER GROUPS AND SIGNED SELMER GROUPS OF ELLIPTIC MODULAR FORMS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 105 / Issue 3 / June 2022
- Published online by Cambridge University Press:
- 19 April 2022, pp. 419-430
- Print publication:
- June 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On the algebraicity about the Hodge numbers of the Hilbert schemes of algebraic surfaces
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 65 / Issue 2 / May 2022
- Published online by Cambridge University Press:
- 19 April 2022, pp. 392-403
-
- Article
- Export citation
ALTERNATING CIRCULAR SUMS OF BINOMIAL COEFFICIENTS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 106 / Issue 3 / December 2022
- Published online by Cambridge University Press:
- 13 April 2022, pp. 385-395
- Print publication:
- December 2022
-
- Article
- Export citation
ON A PROPERNESS OF THE HILBERT EIGENVARIETY AT INTEGRAL WEIGHTS: THE CASE OF QUADRATIC RESIDUE FIELDS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 22 / Issue 6 / November 2023
- Published online by Cambridge University Press:
- 08 April 2022, pp. 2645-2716
- Print publication:
- November 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation