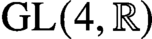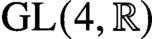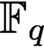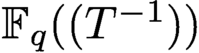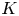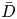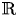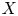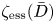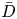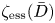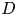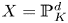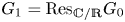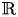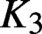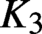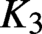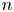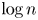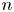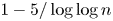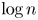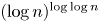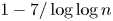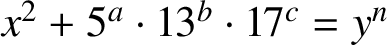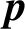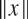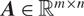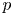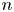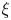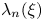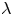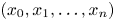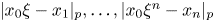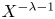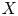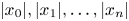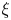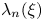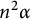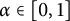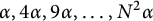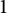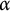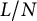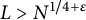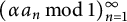Refine listing
Actions for selected content:
2812 results in 11xxx
An orthogonality relation for
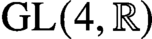 $\mathrm {GL}(4, \mathbb R) $ (with an appendix by Bingrong Huang)
$\mathrm {GL}(4, \mathbb R) $ (with an appendix by Bingrong Huang)
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 9 / 2021
- Published online by Cambridge University Press:
- 07 June 2021, e47
-
- Article
-
- You have access
- Open access
- Export citation
MAHLER’S AND KOKSMA’S CLASSIFICATIONS IN FIELDS OF POWER SERIES
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 246 / June 2022
- Published online by Cambridge University Press:
- 07 June 2021, pp. 355-371
- Print publication:
- June 2022
-
- Article
- Export citation
Successive minima and asymptotic slopes in Arakelov geometry
- Part of
-
- Journal:
- Compositio Mathematica / Volume 157 / Issue 6 / June 2021
- Published online by Cambridge University Press:
- 10 June 2021, pp. 1302-1339
- Print publication:
- June 2021
-
- Article
- Export citation
GENERATORS OF FINITE FIELDS WITH PRESCRIBED TRACES
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 112 / Issue 3 / June 2022
- Published online by Cambridge University Press:
- 27 May 2021, pp. 355-366
- Print publication:
- June 2022
-
- Article
- Export citation
Corrigendum: On the cuspidal cohomology of S-arithmetic subgroups of reductive groups over number fields
- Part of
-
- Journal:
- Compositio Mathematica / Volume 157 / Issue 6 / June 2021
- Published online by Cambridge University Press:
- 26 May 2021, pp. 1207-1210
- Print publication:
- June 2021
-
- Article
-
- You have access
- HTML
- Export citation
Une note sur la densité des zéros des sommes partielles de la fonction zeta de Dedekind sur un corps quadratique
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 65 / Issue 2 / June 2022
- Published online by Cambridge University Press:
- 24 May 2021, pp. 409-415
- Print publication:
- June 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Hyperbolic tessellations and generators of
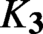 ${K}_{\textbf {3}}$ for imaginary quadratic fields
${K}_{\textbf {3}}$ for imaginary quadratic fields
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 9 / 2021
- Published online by Cambridge University Press:
- 24 May 2021, e40
-
- Article
-
- You have access
- Open access
- Export citation
Most permutations power to a cycle of small prime length
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 64 / Issue 2 / May 2021
- Published online by Cambridge University Press:
- 24 May 2021, pp. 234-246
-
- Article
- Export citation
SOLUTIONS TO A LEBESGUE–NAGELL EQUATION
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 105 / Issue 1 / February 2022
- Published online by Cambridge University Press:
- 24 May 2021, pp. 19-30
- Print publication:
- February 2022
-
- Article
- Export citation
ELLIPTIC CURVES AND
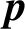 $\boldsymbol {p}$-ADIC ELLIPTIC TRANSCENDENCE
$\boldsymbol {p}$-ADIC ELLIPTIC TRANSCENDENCE
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 105 / Issue 1 / February 2022
- Published online by Cambridge University Press:
- 21 May 2021, pp. 31-36
- Print publication:
- February 2022
-
- Article
- Export citation
NOTE ON THE p-DIVISIBILITY OF CLASS NUMBERS OF AN INFINITE FAMILY OF IMAGINARY QUADRATIC FIELDS
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 64 / Issue 2 / May 2022
- Published online by Cambridge University Press:
- 20 May 2021, pp. 352-357
- Print publication:
- May 2022
-
- Article
- Export citation
Solving equations in dense Sidon sets
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 173 / Issue 1 / July 2022
- Published online by Cambridge University Press:
- 19 May 2021, pp. 25-34
- Print publication:
- July 2022
-
- Article
- Export citation
The effective Shafarevich conjecture for abelian varieties of
 ${\text {GL}_{2}}$-type
${\text {GL}_{2}}$-type
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 9 / 2021
- Published online by Cambridge University Press:
- 19 May 2021, e39
-
- Article
-
- You have access
- Open access
- Export citation
Multiplicatively badly approximable matrices up to logarithmic factors
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 172 / Issue 3 / May 2022
- Published online by Cambridge University Press:
- 17 May 2021, pp. 685-703
- Print publication:
- May 2022
-
- Article
- Export citation
Thue equations that simultaneously fail the Hasse principle
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 172 / Issue 3 / May 2022
- Published online by Cambridge University Press:
- 17 May 2021, pp. 617-626
- Print publication:
- May 2022
-
- Article
- Export citation
Prime geodesics and averages of the Zagier L-series
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 172 / Issue 3 / May 2022
- Published online by Cambridge University Press:
- 11 May 2021, pp. 705-728
- Print publication:
- May 2022
-
- Article
- Export citation
On the cohomology of Kobayashi’s plus/minus norm groups and applications
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 173 / Issue 1 / July 2022
- Published online by Cambridge University Press:
- 11 May 2021, pp. 1-24
- Print publication:
- July 2022
-
- Article
- Export citation
On the distribution of the digits of quotients of integers and primes
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 65 / Issue 2 / June 2022
- Published online by Cambridge University Press:
- 11 May 2021, pp. 279-295
- Print publication:
- June 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On simultaneous rational approximation to a p-adic number and its integral powers, II
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 64 / Issue 2 / May 2021
- Published online by Cambridge University Press:
- 07 May 2021, pp. 317-337
-
- Article
- Export citation
On the triple correlations of fractional parts of
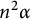 $n^2\alpha $
$n^2\alpha $
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 74 / Issue 5 / October 2022
- Published online by Cambridge University Press:
- 04 May 2021, pp. 1347-1384
- Print publication:
- October 2022
-
- Article
- Export citation