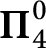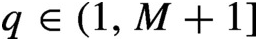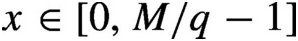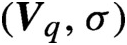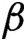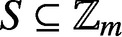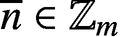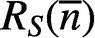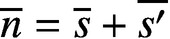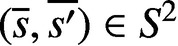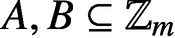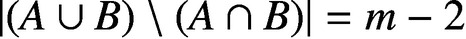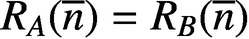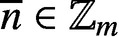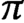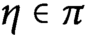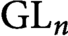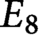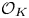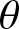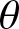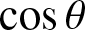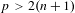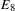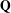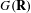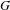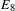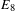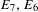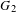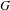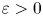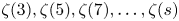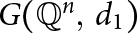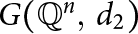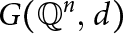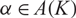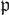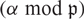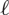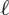Refine listing
Actions for selected content:
2812 results in 11xxx
G-torseurs en théorie de Hodge p-adique
- Part of
-
- Journal:
- Compositio Mathematica / Volume 156 / Issue 10 / October 2020
- Published online by Cambridge University Press:
- 24 November 2020, pp. 2076-2110
- Print publication:
- October 2020
-
- Article
- Export citation
CONGRUENCE PRIMES FOR SIEGEL MODULAR FORMS OF PARAMODULAR LEVEL AND APPLICATIONS TO THE BLOCH–KATO CONJECTURE
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 63 / Issue 3 / September 2021
- Published online by Cambridge University Press:
- 29 September 2020, pp. 660-681
- Print publication:
- September 2021
-
- Article
- Export citation
Some complexity results in the theory of normal numbers
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 74 / Issue 1 / February 2022
- Published online by Cambridge University Press:
- 28 September 2020, pp. 170-198
- Print publication:
- February 2022
-
- Article
- Export citation
On the specification property and synchronization of unique q-expansions
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 9 / September 2021
- Published online by Cambridge University Press:
- 28 September 2020, pp. 2659-2705
- Print publication:
- September 2021
-
- Article
- Export citation
Arithmeticity of discrete subgroups
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 9 / September 2021
- Published online by Cambridge University Press:
- 28 September 2020, pp. 2561-2590
- Print publication:
- September 2021
-
- Article
- Export citation
PARTITIONS OF
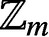 $\mathbb {Z}_m$ WITH IDENTICAL REPRESENTATION FUNCTION
$\mathbb {Z}_m$ WITH IDENTICAL REPRESENTATION FUNCTION
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 103 / Issue 2 / April 2021
- Published online by Cambridge University Press:
- 22 September 2020, pp. 204-209
- Print publication:
- April 2021
-
- Article
- Export citation
Fourier coefficients of minimal and next-to-minimal automorphic representations of simply-laced groups
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 74 / Issue 1 / February 2022
- Published online by Cambridge University Press:
- 21 September 2020, pp. 122-169
- Print publication:
- February 2022
-
- Article
-
- You have access
- Open access
- Export citation
THE ROGERS–RAMANUJAN CONTINUED FRACTION AND RELATED ETA-QUOTIENT REPRESENTATIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 103 / Issue 2 / April 2021
- Published online by Cambridge University Press:
- 17 September 2020, pp. 248-259
- Print publication:
- April 2021
-
- Article
- Export citation
There are no universal ternary quadratic forms over biquadratic fields
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 63 / Issue 3 / August 2020
- Published online by Cambridge University Press:
- 16 September 2020, pp. 861-912
-
- Article
- Export citation
ON
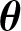 $\boldsymbol{\theta} $-CONGRUENT NUMBERS OVER REAL NUMBER FIELDS
$\boldsymbol{\theta} $-CONGRUENT NUMBERS OVER REAL NUMBER FIELDS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 103 / Issue 2 / April 2021
- Published online by Cambridge University Press:
- 09 September 2020, pp. 218-229
- Print publication:
- April 2021
-
- Article
- Export citation
DISTRIBUTION OF THE DIVISOR FUNCTION AT CONSECUTIVE INTEGERS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 103 / Issue 2 / April 2021
- Published online by Cambridge University Press:
- 09 September 2020, pp. 244-247
- Print publication:
- April 2021
-
- Article
- Export citation
Dyson’s rank, overpartitions, and universal mock theta functions
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 64 / Issue 3 / September 2021
- Published online by Cambridge University Press:
- 07 September 2020, pp. 687-696
- Print publication:
- September 2021
-
- Article
- Export citation
GLOBALLY REALIZABLE COMPONENTS OF LOCAL DEFORMATION RINGS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 21 / Issue 2 / March 2022
- Published online by Cambridge University Press:
- 03 September 2020, pp. 533-602
- Print publication:
- March 2022
-
- Article
- Export citation
Arithmetic diagonal cycles on unitary Shimura varieties
- Part of
-
- Journal:
- Compositio Mathematica / Volume 156 / Issue 9 / September 2020
- Published online by Cambridge University Press:
- 27 October 2020, pp. 1745-1824
- Print publication:
- September 2020
-
- Article
- Export citation
THE MINIMAL MODULAR FORM ON QUATERNIONIC
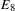 $E_{8}$
$E_{8}$
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 21 / Issue 2 / March 2022
- Published online by Cambridge University Press:
- 20 August 2020, pp. 603-636
- Print publication:
- March 2022
-
- Article
- Export citation
LINEAR RELATIONS AND INTEGRABILITY FOR CLUSTER ALGEBRAS FROM AFFINE QUIVERS
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 63 / Issue 3 / September 2021
- Published online by Cambridge University Press:
- 13 August 2020, pp. 584-621
- Print publication:
- September 2021
-
- Article
- Export citation
Local intertwining relation for metaplectic groups
- Part of
-
- Journal:
- Compositio Mathematica / Volume 156 / Issue 8 / August 2020
- Published online by Cambridge University Press:
- 01 October 2020, pp. 1560-1594
- Print publication:
- August 2020
-
- Article
- Export citation
A note on the number of irrational odd zeta values
- Part of
-
- Journal:
- Compositio Mathematica / Volume 156 / Issue 8 / August 2020
- Published online by Cambridge University Press:
- 09 October 2020, pp. 1699-1717
- Print publication:
- August 2020
-
- Article
- Export citation
On Single-Distance Graphs on the Rational Points in Euclidean Spaces
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 64 / Issue 1 / March 2021
- Published online by Cambridge University Press:
- 29 July 2020, pp. 13-24
- Print publication:
- March 2021
-
- Article
- Export citation
REDUCTIONS OF POINTS ON ALGEBRAIC GROUPS, II
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 63 / Issue 2 / May 2021
- Published online by Cambridge University Press:
- 28 July 2020, pp. 484-502
- Print publication:
- May 2021
-
- Article
-
- You have access
- Open access
- Export citation