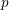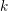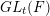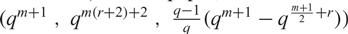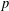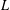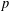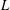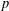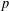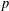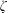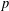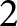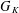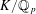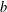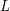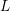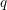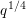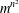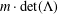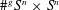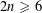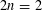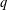Refine listing
Actions for selected content:
2812 results in 11xxx
CHARACTERIZING THE MOD-
 $\ell$ LOCAL LANGLANDS CORRESPONDENCE BY NILPOTENT GAMMA FACTORS
$\ell$ LOCAL LANGLANDS CORRESPONDENCE BY NILPOTENT GAMMA FACTORS
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 244 / December 2021
- Published online by Cambridge University Press:
- 12 May 2020, pp. 119-135
- Print publication:
- December 2021
-
- Article
- Export citation
NONBINARY DELSARTE–GOETHALS CODES AND FINITE SEMIFIELDS
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 62 / Issue S1 / December 2020
- Published online by Cambridge University Press:
- 07 May 2020, pp. S186-S205
- Print publication:
- December 2020
-
- Article
- Export citation
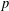 $p$-ADIC
$p$-ADIC 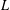 $L$-FUNCTIONS FOR UNITARY GROUPS
$L$-FUNCTIONS FOR UNITARY GROUPS
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 8 / 2020
- Published online by Cambridge University Press:
- 06 May 2020, e9
-
- Article
-
- You have access
- Open access
- Export citation
Corrigendum: On the probabilities of local behaviors in abelian field extensions
- Part of
-
- Journal:
- Compositio Mathematica / Volume 156 / Issue 5 / May 2020
- Published online by Cambridge University Press:
- 15 May 2020, p. 1078
- Print publication:
- May 2020
-
- Article
-
- You have access
- HTML
- Export citation
Semistable models of elliptic curves over residue characteristic 2
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 64 / Issue 1 / March 2021
- Published online by Cambridge University Press:
- 29 April 2020, pp. 154-162
- Print publication:
- March 2021
-
- Article
- Export citation
ON THE ARITHMETIC STRUCTURE OF RATIONAL NUMBERS IN THE CANTOR SET
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 103 / Issue 1 / February 2021
- Published online by Cambridge University Press:
- 27 April 2020, pp. 22-27
- Print publication:
- February 2021
-
- Article
- Export citation
ON THE IRREDUCIBLE COMPONENTS OF SOME CRYSTALLINE DEFORMATION RINGS
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 8 / 2020
- Published online by Cambridge University Press:
- 24 April 2020, e22
-
- Article
-
- You have access
- Open access
- Export citation
Rational lines on cubic hypersurfaces
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 171 / Issue 1 / July 2021
- Published online by Cambridge University Press:
- 24 April 2020, pp. 99-112
- Print publication:
- July 2021
-
- Article
-
- You have access
- Open access
- Export citation
ON SOME QUESTIONS OF PARTITIO NUMERORUM: TRES CUBI
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 63 / Issue 1 / January 2021
- Published online by Cambridge University Press:
- 21 April 2020, pp. 223-244
- Print publication:
- January 2021
-
- Article
- Export citation
NOTE ON FOURIER–STIELTJES COEFFICIENTS OF COIN-TOSSING MEASURES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 102 / Issue 3 / December 2020
- Published online by Cambridge University Press:
- 20 April 2020, pp. 479-489
- Print publication:
- December 2020
-
- Article
- Export citation
Motohashi’s fourth moment identity for non-archimedean test functions and applications
- Part of
-
- Journal:
- Compositio Mathematica / Volume 156 / Issue 5 / May 2020
- Published online by Cambridge University Press:
- 17 April 2020, pp. 1004-1038
- Print publication:
- May 2020
-
- Article
- Export citation
Lower bounds for Maass forms on semisimple groups
- Part of
-
- Journal:
- Compositio Mathematica / Volume 156 / Issue 5 / May 2020
- Published online by Cambridge University Press:
- 17 April 2020, pp. 959-1003
- Print publication:
- May 2020
-
- Article
- Export citation
The Trace Form Over Cyclic Number Fields
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 73 / Issue 4 / August 2021
- Published online by Cambridge University Press:
- 14 April 2020, pp. 947-969
- Print publication:
- August 2021
-
- Article
- Export citation
Local Rankin–Selberg integrals for Speh representations
- Part of
-
- Journal:
- Compositio Mathematica / Volume 156 / Issue 5 / May 2020
- Published online by Cambridge University Press:
- 13 April 2020, pp. 908-945
- Print publication:
- May 2020
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
CLASSIFICATION OF THE SUBLATTICES OF A LATTICE
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 103 / Issue 1 / February 2021
- Published online by Cambridge University Press:
- 13 April 2020, pp. 50-61
- Print publication:
- February 2021
-
- Article
- Export citation
ON THE COHOMOLOGY OF TORELLI GROUPS
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 8 / 2020
- Published online by Cambridge University Press:
- 13 April 2020, e7
-
- Article
-
- You have access
- Open access
- Export citation
A TRUNCATED IDENTITY OF EULER AND RELATED
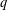 $q$-CONGRUENCES
$q$-CONGRUENCES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 102 / Issue 3 / December 2020
- Published online by Cambridge University Press:
- 08 April 2020, pp. 353-359
- Print publication:
- December 2020
-
- Article
- Export citation
THE DE BRUIJN–NEWMAN CONSTANT IS NON-NEGATIVE
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 8 / 2020
- Published online by Cambridge University Press:
- 06 April 2020, e6
-
- Article
-
- You have access
- Open access
- Export citation
The Modularity of Special Cycles on Orthogonal Shimura Varieties over Totally Real Fields under the Beilinson–Bloch Conjecture
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 64 / Issue 1 / March 2021
- Published online by Cambridge University Press:
- 30 March 2020, pp. 39-53
- Print publication:
- March 2021
-
- Article
- Export citation
VANISHING COEFFICIENTS IN QUOTIENTS OF THETA FUNCTIONS OF MODULUS FIVE
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 102 / Issue 3 / December 2020
- Published online by Cambridge University Press:
- 27 March 2020, pp. 387-398
- Print publication:
- December 2020
-
- Article
- Export citation