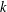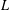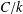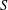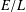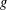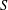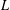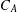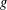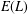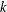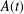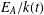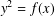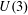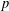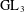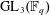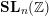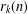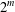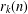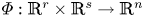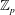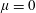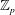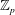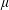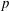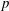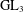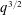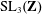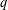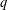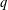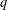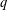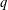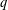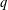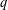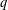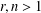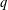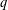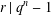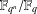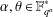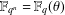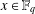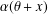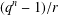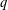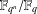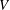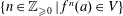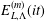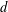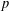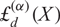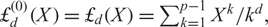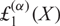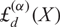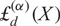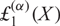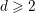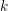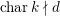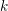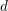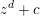Refine listing
Actions for selected content:
2812 results in 11xxx
ON INTEGRAL POINTS ON ISOTRIVIAL ELLIPTIC CURVES OVER FUNCTION FIELDS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 102 / Issue 2 / October 2020
- Published online by Cambridge University Press:
- 27 March 2020, pp. 177-185
- Print publication:
- October 2020
-
- Article
-
- You have access
- Export citation
SERRE WEIGHTS AND BREUIL’S LATTICE CONJECTURE IN DIMENSION THREE
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 8 / 2020
- Published online by Cambridge University Press:
- 25 March 2020, e5
-
- Article
-
- You have access
- Open access
- Export citation
RELATIVE UNITARY RZ-SPACES AND THE ARITHMETIC FUNDAMENTAL LEMMA
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 21 / Issue 1 / January 2022
- Published online by Cambridge University Press:
- 24 March 2020, pp. 241-301
- Print publication:
- January 2022
-
- Article
- Export citation
Stability in the high-dimensional cohomology of congruence subgroups
- Part of
-
- Journal:
- Compositio Mathematica / Volume 156 / Issue 4 / April 2020
- Published online by Cambridge University Press:
- 24 March 2020, pp. 822-861
- Print publication:
- April 2020
-
- Article
- Export citation
SUMS OF SQUARES AND PARTITION CONGRUENCES
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 111 / Issue 2 / October 2021
- Published online by Cambridge University Press:
- 18 March 2020, pp. 249-267
- Print publication:
- October 2021
-
- Article
- Export citation
Nonsingular bilinear maps revisited
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 151 / Issue 1 / February 2021
- Published online by Cambridge University Press:
- 17 March 2020, pp. 377-390
- Print publication:
- February 2021
-
- Article
- Export citation
ISOGENIES OF ABELIAN VARIETIES IN CRYPTOGRAPHY
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 101 / Issue 3 / June 2020
- Published online by Cambridge University Press:
- 16 March 2020, pp. 508-509
- Print publication:
- June 2020
-
- Article
-
- You have access
- Export citation
Growth of Fine Selmer Groups in Infinite Towers
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 63 / Issue 4 / December 2020
- Published online by Cambridge University Press:
- 13 March 2020, pp. 921-936
- Print publication:
- December 2020
-
- Article
- Export citation
PERIODIC TWISTS OF
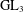 $\operatorname{GL}_{3}$-AUTOMORPHIC FORMS
$\operatorname{GL}_{3}$-AUTOMORPHIC FORMS
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 8 / 2020
- Published online by Cambridge University Press:
- 12 March 2020, e15
-
- Article
-
- You have access
- Open access
- Export citation
WILD RAMIFICATION IN TRINOMIAL EXTENSIONS AND GALOIS GROUPS
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 63 / Issue 1 / January 2021
- Published online by Cambridge University Press:
- 12 March 2020, pp. 106-120
- Print publication:
- January 2021
-
- Article
- Export citation
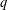 $q$-DEFORMED RATIONALS AND
$q$-DEFORMED RATIONALS AND 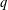 $q$-CONTINUED FRACTIONS
$q$-CONTINUED FRACTIONS
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 8 / 2020
- Published online by Cambridge University Press:
- 06 March 2020, e13
-
- Article
-
- You have access
- Open access
- Export citation
FINITE FIELD EXTENSIONS WITH THE LINE OR TRANSLATE PROPERTY FOR
 $r$-PRIMITIVE ELEMENTS
$r$-PRIMITIVE ELEMENTS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 111 / Issue 3 / December 2021
- Published online by Cambridge University Press:
- 02 March 2020, pp. 313-319
- Print publication:
- December 2021
-
- Article
-
- You have access
- Open access
- Export citation
A Gap Principle for Subvarieties with Finitely Many Periodic Points
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 63 / Issue 2 / June 2020
- Published online by Cambridge University Press:
- 28 February 2020, pp. 382-392
- Print publication:
- June 2020
-
- Article
-
- You have access
- Export citation
ON A LATTICE GENERALISATION OF THE LOGARITHM AND A DEFORMATION OF THE DEDEKIND ETA FUNCTION
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 102 / Issue 1 / August 2020
- Published online by Cambridge University Press:
- 20 February 2020, pp. 118-125
- Print publication:
- August 2020
-
- Article
-
- You have access
- Open access
- Export citation
Automorphisms of automatic shifts
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 5 / May 2021
- Published online by Cambridge University Press:
- 20 February 2020, pp. 1530-1559
- Print publication:
- May 2021
-
- Article
- Export citation
Attractors associated to a family of hyperbolic
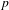 $p$ -adic plane automorphisms
$p$ -adic plane automorphisms
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 6 / June 2021
- Published online by Cambridge University Press:
- 20 February 2020, pp. 1867-1882
- Print publication:
- June 2021
-
- Article
- Export citation
ON SEMIGROUP ORBITS OF POLYNOMIALS AND MULTIPLICATIVE ORDERS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 102 / Issue 3 / December 2020
- Published online by Cambridge University Press:
- 20 February 2020, pp. 365-373
- Print publication:
- December 2020
-
- Article
- Export citation
POWER PARTITIONS AND SEMI-
 $m$-FIBONACCI PARTITIONS
$m$-FIBONACCI PARTITIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 102 / Issue 3 / December 2020
- Published online by Cambridge University Press:
- 20 February 2020, pp. 418-429
- Print publication:
- December 2020
-
- Article
- Export citation
GENERALIZED FINITE POLYLOGARITHMS
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 63 / Issue 1 / January 2021
- Published online by Cambridge University Press:
- 19 February 2020, pp. 66-80
- Print publication:
- January 2021
-
- Article
- Export citation
Gonality of dynatomic curves and strong uniform boundedness of preperiodic points
- Part of
-
- Journal:
- Compositio Mathematica / Volume 156 / Issue 4 / April 2020
- Published online by Cambridge University Press:
- 17 February 2020, pp. 733-743
- Print publication:
- April 2020
-
- Article
- Export citation