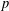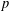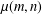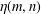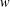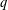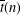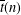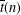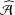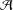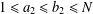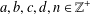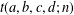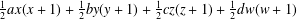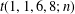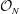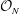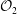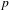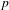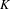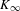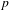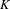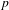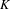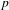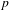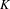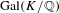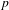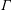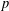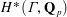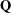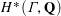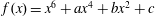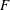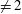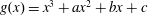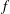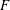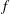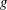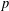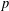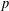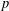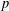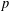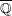Refine listing
Actions for selected content:
2812 results in 11xxx
ON THE EXISTENCE OF ADMISSIBLE SUPERSINGULAR REPRESENTATIONS OF
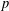 $p$-ADIC REDUCTIVE GROUPS
$p$-ADIC REDUCTIVE GROUPS
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 8 / 2020
- Published online by Cambridge University Press:
- 13 January 2020, e2
-
- Article
-
- You have access
- Open access
- Export citation
RANK GENERATING FUNCTIONS FOR ODD-BALANCED UNIMODAL SEQUENCES, QUANTUM JACOBI FORMS, AND MOCK JACOBI FORMS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 109 / Issue 2 / October 2020
- Published online by Cambridge University Press:
- 10 January 2020, pp. 157-175
- Print publication:
- October 2020
-
- Article
-
- You have access
- Export citation
CLOSED FORMS FOR DEGENERATE BERNOULLI POLYNOMIALS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 101 / Issue 2 / April 2020
- Published online by Cambridge University Press:
- 10 January 2020, pp. 207-217
- Print publication:
- April 2020
-
- Article
-
- You have access
- Export citation
INFINITE FAMILIES OF CONGRUENCES FOR OVERPARTITIONS WITH RESTRICTED ODD DIFFERENCES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 102 / Issue 1 / August 2020
- Published online by Cambridge University Press:
- 08 January 2020, pp. 59-66
- Print publication:
- August 2020
-
- Article
-
- You have access
- Export citation
SOME REMARKS ON MINIMAL ASYMPTOTIC BASES OF ORDER THREE
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 102 / Issue 1 / August 2020
- Published online by Cambridge University Press:
- 08 January 2020, pp. 21-30
- Print publication:
- August 2020
-
- Article
-
- You have access
- Export citation
DERIVATION RELATION FOR FINITE MULTIPLE ZETA VALUES IN
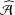 $\widehat{{\mathcal{A}}}$
$\widehat{{\mathcal{A}}}$
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 110 / Issue 2 / April 2021
- Published online by Cambridge University Press:
- 08 January 2020, pp. 260-265
- Print publication:
- April 2021
-
- Article
- Export citation
ROUGH INTEGERS WITH A DIVISOR IN A GIVEN INTERVAL
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 111 / Issue 1 / August 2021
- Published online by Cambridge University Press:
- 08 January 2020, pp. 17-36
- Print publication:
- August 2021
-
- Article
- Export citation
TRANSFORMATION FORMULAS FOR THE NUMBER OF REPRESENTATIONS OF
 $n$ BY LINEAR COMBINATIONS OF FOUR TRIANGULAR NUMBERS
$n$ BY LINEAR COMBINATIONS OF FOUR TRIANGULAR NUMBERS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 102 / Issue 1 / August 2020
- Published online by Cambridge University Press:
- 08 January 2020, pp. 39-49
- Print publication:
- August 2020
-
- Article
-
- You have access
- Export citation
SIMULTANEOUS DYNAMICAL DIOPHANTINE APPROXIMATION IN BETA EXPANSIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 102 / Issue 2 / October 2020
- Published online by Cambridge University Press:
- 08 January 2020, pp. 186-195
- Print publication:
- October 2020
-
- Article
-
- You have access
- Export citation
ON SUMS OF TWO PRIME SQUARES, FOUR PRIME CUBES AND POWERS OF TWO
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 102 / Issue 2 / October 2020
- Published online by Cambridge University Press:
- 08 January 2020, pp. 207-216
- Print publication:
- October 2020
-
- Article
-
- You have access
- Export citation
Slow Continued Fractions and Permutative Representations of
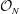 ${\mathcal{O}}_{N}$
${\mathcal{O}}_{N}$
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 63 / Issue 4 / December 2020
- Published online by Cambridge University Press:
- 03 January 2020, pp. 787-801
- Print publication:
- December 2020
-
- Article
- Export citation
HEURISTICS FOR
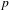 $p$-CLASS TOWERS OF REAL QUADRATIC FIELDS
$p$-CLASS TOWERS OF REAL QUADRATIC FIELDS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 20 / Issue 4 / July 2021
- Published online by Cambridge University Press:
- 26 December 2019, pp. 1429-1452
- Print publication:
- July 2021
-
- Article
- Export citation
DERIVED HECKE ALGEBRA AND COHOMOLOGY OF ARITHMETIC GROUPS
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 7 / 2019
- Published online by Cambridge University Press:
- 23 December 2019, e7
-
- Article
-
- You have access
- Open access
- Export citation
Hausdorff dimension of divergent trajectories on homogeneous spaces
- Part of
-
- Journal:
- Compositio Mathematica / Volume 156 / Issue 2 / February 2020
- Published online by Cambridge University Press:
- 19 December 2019, pp. 340-359
- Print publication:
- February 2020
-
- Article
- Export citation
Belyi’s theorem in characteristic two
- Part of
-
- Journal:
- Compositio Mathematica / Volume 156 / Issue 2 / February 2020
- Published online by Cambridge University Press:
- 18 December 2019, pp. 325-339
- Print publication:
- February 2020
-
- Article
- Export citation
Irregularities in the Distribution of Prime Numbers in a Beatty Sequence
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 63 / Issue 4 / December 2020
- Published online by Cambridge University Press:
- 16 December 2019, pp. 738-743
- Print publication:
- December 2020
-
- Article
- Export citation
On square-free values of large polynomials over the rational function field
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 170 / Issue 2 / March 2021
- Published online by Cambridge University Press:
- 12 December 2019, pp. 247-263
- Print publication:
- March 2021
-
- Article
- Export citation
Galois Groups of Even Sextic Polynomials
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 63 / Issue 3 / September 2020
- Published online by Cambridge University Press:
- 12 December 2019, pp. 670-676
- Print publication:
- September 2020
-
- Article
-
- You have access
- Export citation
ON SPRINDŽUK’S CLASSIFICATION OF
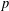 $p$-ADIC NUMBERS
$p$-ADIC NUMBERS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 111 / Issue 2 / October 2021
- Published online by Cambridge University Press:
- 12 December 2019, pp. 221-231
- Print publication:
- October 2021
-
- Article
- Export citation
Linear Independence of Logarithms of Cyclotomic Numbers and a Conjecture of Livingston
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 63 / Issue 1 / March 2020
- Published online by Cambridge University Press:
- 12 December 2019, pp. 31-45
- Print publication:
- March 2020
-
- Article
-
- You have access
- Export citation