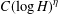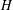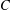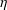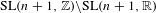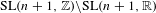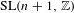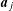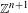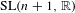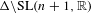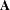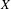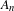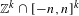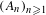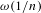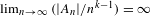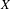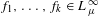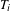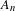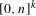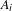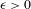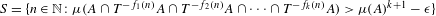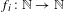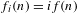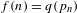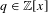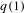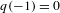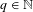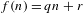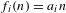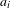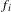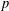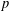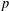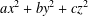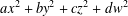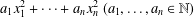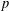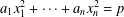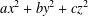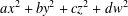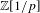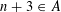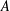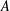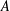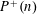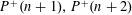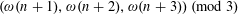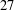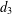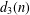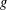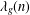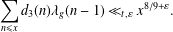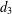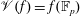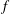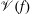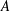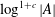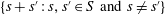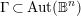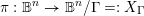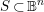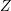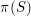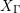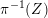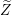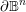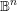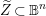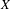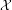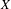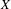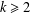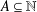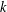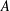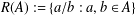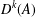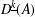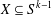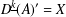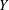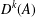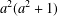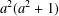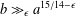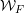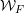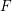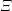Refine listing
Actions for selected content:
2812 results in 11xxx
ALGEBRAIC VALUES OF CERTAIN ANALYTIC FUNCTIONS DEFINED BY A CANONICAL PRODUCT
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 101 / Issue 3 / June 2020
- Published online by Cambridge University Press:
- 08 October 2019, pp. 415-425
- Print publication:
- June 2020
-
- Article
-
- You have access
- Export citation
Equidistribution of Farey sequences on horospheres in covers of
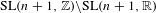 $\text{SL}(n+1,\mathbb{Z})\backslash \text{SL}(n+1,\mathbb{R})$ and applications
$\text{SL}(n+1,\mathbb{Z})\backslash \text{SL}(n+1,\mathbb{R})$ and applications
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 2 / February 2021
- Published online by Cambridge University Press:
- 07 October 2019, pp. 471-493
- Print publication:
- February 2021
-
- Article
- Export citation
A new mean ergodic theorem for tori and recurrences
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 2 / February 2021
- Published online by Cambridge University Press:
- 07 October 2019, pp. 570-577
- Print publication:
- February 2021
-
- Article
- Export citation
Optimal lower bounds for multiple recurrence
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 2 / February 2021
- Published online by Cambridge University Press:
- 07 October 2019, pp. 379-407
- Print publication:
- February 2021
-
- Article
- Export citation
EISENSTEIN–KRONECKER SERIES VIA THE POINCARÉ BUNDLE
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 7 / 2019
- Published online by Cambridge University Press:
- 30 September 2019, e34
-
- Article
-
- You have access
- Open access
- Export citation
PRIME-UNIVERSAL QUADRATIC FORMS
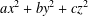 $ax^{2}+by^{2}+cz^{2}$ AND
$ax^{2}+by^{2}+cz^{2}$ AND 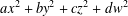 $ax^{2}+by^{2}+cz^{2}+dw^{2}$
$ax^{2}+by^{2}+cz^{2}+dw^{2}$
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 101 / Issue 1 / February 2020
- Published online by Cambridge University Press:
- 27 September 2019, pp. 1-12
- Print publication:
- February 2020
-
- Article
-
- You have access
- Export citation
RIGIDITY FOR RIGID ANALYTIC MOTIVES
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 20 / Issue 4 / July 2021
- Published online by Cambridge University Press:
- 27 September 2019, pp. 1341-1369
- Print publication:
- July 2021
-
- Article
- Export citation
VALUE PATTERNS OF MULTIPLICATIVE FUNCTIONS AND RELATED SEQUENCES
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 7 / 2019
- Published online by Cambridge University Press:
- 26 September 2019, e33
-
- Article
-
- You have access
- Open access
- Export citation
A SHIFTED CONVOLUTION SUM OF
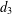 $d_{3}$ AND THE FOURIER COEFFICIENTS OF HECKE–MAASS FORMS II
$d_{3}$ AND THE FOURIER COEFFICIENTS OF HECKE–MAASS FORMS II
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 101 / Issue 3 / June 2020
- Published online by Cambridge University Press:
- 26 September 2019, pp. 401-414
- Print publication:
- June 2020
-
- Article
-
- You have access
- Export citation
Higher-rank Bohr sets and multiplicative diophantine approximation
- Part of
-
- Journal:
- Compositio Mathematica / Volume 155 / Issue 11 / November 2019
- Published online by Cambridge University Press:
- 24 September 2019, pp. 2214-2233
- Print publication:
- November 2019
-
- Article
- Export citation
Value Sets of Sparse Polynomials
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 63 / Issue 1 / March 2020
- Published online by Cambridge University Press:
- 24 September 2019, pp. 187-196
- Print publication:
- March 2020
-
- Article
-
- You have access
- Export citation
The Erdős–Moser Sum-free Set Problem
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 73 / Issue 1 / February 2021
- Published online by Cambridge University Press:
- 23 September 2019, pp. 63-107
- Print publication:
- February 2021
-
- Article
- Export citation
THE EXPLICIT MORDELL CONJECTURE FOR FAMILIES OF CURVES
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 7 / 2019
- Published online by Cambridge University Press:
- 19 September 2019, e31
-
- Article
-
- You have access
- Open access
- Export citation
Zariski closures of images of algebraic subsets under the uniformization map on finite-volume quotients of the complex unit ball
- Part of
-
- Journal:
- Compositio Mathematica / Volume 155 / Issue 11 / November 2019
- Published online by Cambridge University Press:
- 19 September 2019, pp. 2129-2149
- Print publication:
- November 2019
-
- Article
- Export citation
TATE’S CONJECTURE AND THE TATE–SHAFAREVICH GROUP OVER GLOBAL FUNCTION FIELDS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 20 / Issue 3 / May 2021
- Published online by Cambridge University Press:
- 17 September 2019, pp. 1001-1022
- Print publication:
- May 2021
-
- Article
- Export citation
DIRECTIONS SETS: A GENERALISATION OF RATIO SETS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 101 / Issue 3 / June 2020
- Published online by Cambridge University Press:
- 13 September 2019, pp. 389-395
- Print publication:
- June 2020
-
- Article
-
- You have access
- Export citation
GAPS BETWEEN DIVISIBLE TERMS IN
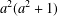 $a^{2}(a^{2}+1)$
$a^{2}(a^{2}+1)$
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 101 / Issue 3 / June 2020
- Published online by Cambridge University Press:
- 13 September 2019, pp. 396-400
- Print publication:
- June 2020
-
- Article
-
- You have access
- Export citation
Continued fractions, the Chen–Stein method and extreme value theory
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 2 / February 2021
- Published online by Cambridge University Press:
- 06 September 2019, pp. 461-470
- Print publication:
- February 2021
-
- Article
- Export citation
Local Langlands correspondence and ramification for Carayol representations
- Part of
-
- Journal:
- Compositio Mathematica / Volume 155 / Issue 10 / October 2019
- Published online by Cambridge University Press:
- 06 September 2019, pp. 1959-2038
- Print publication:
- October 2019
-
- Article
-
- You have access
- HTML
- Export citation
Large prime factors on short intervals
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 170 / Issue 1 / January 2021
- Published online by Cambridge University Press:
- 05 September 2019, pp. 1-50
- Print publication:
- January 2021
-
- Article
- Export citation