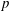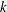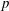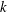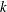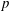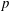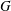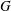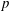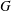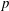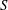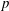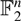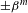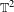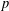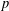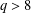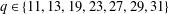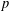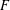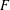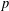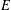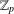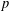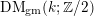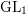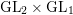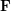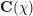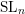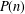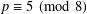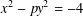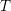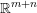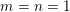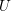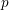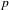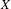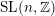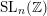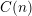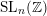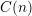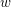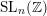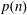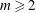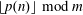Refine listing
Actions for selected content:
2812 results in 11xxx
Retract Rationality and Algebraic Tori
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 63 / Issue 1 / March 2020
- Published online by Cambridge University Press:
- 18 July 2019, pp. 173-186
- Print publication:
- March 2020
-
- Article
-
- You have access
- Export citation
Triforce and corners
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 169 / Issue 1 / July 2020
- Published online by Cambridge University Press:
- 12 July 2019, pp. 209-223
- Print publication:
- July 2020
-
- Article
- Export citation
Generic point equivalence and Pisot numbers
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 40 / Issue 12 / December 2020
- Published online by Cambridge University Press:
- 11 July 2019, pp. 3169-3180
- Print publication:
- December 2020
-
- Article
- Export citation
Fast and slow points of Birkhoff sums
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 40 / Issue 12 / December 2020
- Published online by Cambridge University Press:
- 11 July 2019, pp. 3236-3256
- Print publication:
- December 2020
-
- Article
- Export citation
APPLICATIONS OF LERCH’S THEOREM TO PERMUTATIONS OF QUADRATIC RESIDUES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 100 / Issue 3 / December 2019
- Published online by Cambridge University Press:
- 10 July 2019, pp. 362-371
- Print publication:
- December 2019
-
- Article
-
- You have access
- Export citation
A NEW PROOF OF THE CARLITZ–LUTZ THEOREM
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 101 / Issue 1 / February 2020
- Published online by Cambridge University Press:
- 10 July 2019, pp. 56-60
- Print publication:
- February 2020
-
- Article
-
- You have access
- Export citation
PERMUTATION POLYNOMIALS OF DEGREE 8 OVER FINITE FIELDS OF ODD CHARACTERISTIC
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 101 / Issue 1 / February 2020
- Published online by Cambridge University Press:
- 09 July 2019, pp. 40-55
- Print publication:
- February 2020
-
- Article
-
- You have access
- Export citation
ON THE EULER CHARACTERISTICS OF SIGNED SELMER GROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 101 / Issue 2 / April 2020
- Published online by Cambridge University Press:
- 09 July 2019, pp. 238-246
- Print publication:
- April 2020
-
- Article
-
- You have access
- Export citation
Affine quadrics and the Picard group of the motivic category
- Part of
-
- Journal:
- Compositio Mathematica / Volume 155 / Issue 8 / August 2019
- Published online by Cambridge University Press:
- 04 July 2019, pp. 1500-1520
- Print publication:
- August 2019
-
- Article
- Export citation
Burgess-like subconvexity for
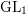 $\text{GL}_{1}$
$\text{GL}_{1}$
- Part of
-
- Journal:
- Compositio Mathematica / Volume 155 / Issue 8 / August 2019
- Published online by Cambridge University Press:
- 04 July 2019, pp. 1457-1499
- Print publication:
- August 2019
-
- Article
- Export citation
Le principe de Hasse pour les espaces homogènes : réduction au cas des stabilisateurs finis
- Part of
-
- Journal:
- Compositio Mathematica / Volume 155 / Issue 8 / August 2019
- Published online by Cambridge University Press:
- 04 July 2019, pp. 1568-1593
- Print publication:
- August 2019
-
- Article
- Export citation
PERIODS OF DUCCI SEQUENCES AND ODD SOLUTIONS TO A PELLIAN EQUATION
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 100 / Issue 2 / October 2019
- Published online by Cambridge University Press:
- 03 July 2019, pp. 201-205
- Print publication:
- October 2019
-
- Article
-
- You have access
- Open access
- Export citation
The sets of Dirichlet non-improvable numbers versus well-approximable numbers
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 40 / Issue 12 / December 2020
- Published online by Cambridge University Press:
- 27 June 2019, pp. 3217-3235
- Print publication:
- December 2020
-
- Article
- Export citation
An inhomogeneous Dirichlet theorem via shrinking targets
- Part of
-
- Journal:
- Compositio Mathematica / Volume 155 / Issue 7 / July 2019
- Published online by Cambridge University Press:
- 25 June 2019, pp. 1402-1423
- Print publication:
- July 2019
-
- Article
- Export citation
Families of Picard modular forms and an application to the Bloch–Kato conjecture
- Part of
-
- Journal:
- Compositio Mathematica / Volume 155 / Issue 7 / July 2019
- Published online by Cambridge University Press:
- 25 June 2019, pp. 1327-1401
- Print publication:
- July 2019
-
- Article
- Export citation
THE DYNAMICAL MORDELL–LANG CONJECTURE FOR ENDOMORPHISMS OF SEMIABELIAN VARIETIES DEFINED OVER FIELDS OF POSITIVE CHARACTERISTIC
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 20 / Issue 2 / March 2021
- Published online by Cambridge University Press:
- 24 June 2019, pp. 669-698
- Print publication:
- March 2021
-
- Article
- Export citation
ON LOCAL FIELDS GENERATED BY DIVISION VALUES OF FORMAL DRINFELD MODULES
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 62 / Issue 2 / May 2020
- Published online by Cambridge University Press:
- 14 June 2019, pp. 459-472
- Print publication:
- May 2020
-
- Article
-
- You have access
- Export citation
Words have bounded width in
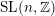 $\operatorname{SL}(n,\mathbb{Z})$
$\operatorname{SL}(n,\mathbb{Z})$
- Part of
-
- Journal:
- Compositio Mathematica / Volume 155 / Issue 7 / July 2019
- Published online by Cambridge University Press:
- 13 June 2019, pp. 1245-1258
- Print publication:
- July 2019
-
- Article
- Export citation
Automatic Sequences and Generalised Polynomials
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 72 / Issue 2 / April 2020
- Published online by Cambridge University Press:
- 13 June 2019, pp. 392-426
- Print publication:
- April 2020
-
- Article
-
- You have access
- Export citation
REFINED SWAN CONDUCTORS
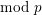 $\text{mod}~p$ OF ONE-DIMENSIONAL GALOIS REPRESENTATIONS
$\text{mod}~p$ OF ONE-DIMENSIONAL GALOIS REPRESENTATIONS
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 236 / December 2019
- Published online by Cambridge University Press:
- 03 June 2019, pp. 134-182
- Print publication:
- December 2019
-
- Article
-
- You have access
- HTML
- Export citation