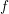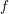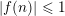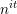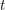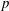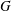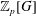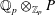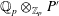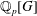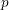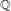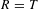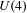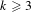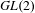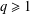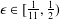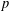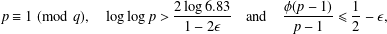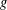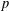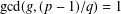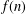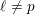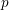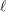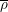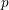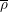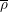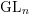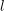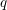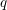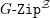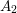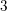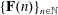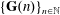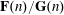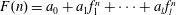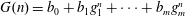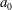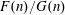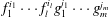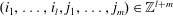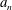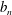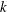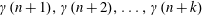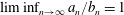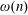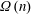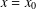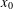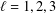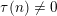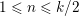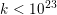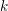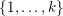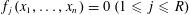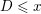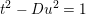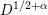Refine listing
Actions for selected content:
2813 results in 11xxx
A new proof of Halász’s theorem, and its consequences
- Part of
-
- Journal:
- Compositio Mathematica / Volume 155 / Issue 1 / January 2019
- Published online by Cambridge University Press:
- 23 November 2018, pp. 126-163
- Print publication:
- January 2019
-
- Article
- Export citation
Szemerédi's Theorem in the Primes
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 62 / Issue 2 / May 2019
- Published online by Cambridge University Press:
- 19 November 2018, pp. 443-457
-
- Article
- Export citation
A Modular André–Oort Statement with Derivatives
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 62 / Issue 2 / May 2019
- Published online by Cambridge University Press:
- 16 November 2018, pp. 323-365
-
- Article
- Export citation
A Generalization of a Theorem of Swan with Applications to Iwasawa Theory
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 72 / Issue 3 / June 2020
- Published online by Cambridge University Press:
- 16 November 2018, pp. 656-675
- Print publication:
- June 2020
-
- Article
-
- You have access
- Export citation
ON THE GALOIS STRUCTURE OF ARITHMETIC COHOMOLOGY I: COMPACTLY SUPPORTED
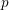 $p$-ADIC COHOMOLOGY
$p$-ADIC COHOMOLOGY
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 239 / September 2020
- Published online by Cambridge University Press:
- 16 November 2018, pp. 294-321
- Print publication:
- September 2020
-
- Article
-
- You have access
- HTML
- Export citation
EULER SYSTEMS FOR HILBERT MODULAR SURFACES
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 6 / 2018
- Published online by Cambridge University Press:
- 15 November 2018, e23
-
- Article
-
- You have access
- Open access
- Export citation
SYMMETRIC POWER CONGRUENCE IDEALS AND SELMER GROUPS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 19 / Issue 5 / September 2020
- Published online by Cambridge University Press:
- 14 November 2018, pp. 1521-1572
- Print publication:
- September 2020
-
- Article
- Export citation
BEYOND ENDOSCOPY VIA THE TRACE FORMULA – IIITHE STANDARD REPRESENTATION
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 19 / Issue 4 / July 2020
- Published online by Cambridge University Press:
- 12 November 2018, pp. 1349-1387
- Print publication:
- July 2020
-
- Article
- Export citation
QUADRATIC NONRESIDUES AND NONPRIMITIVE ROOTS SATISFYING A COPRIMALITY CONDITION
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 99 / Issue 2 / April 2019
- Published online by Cambridge University Press:
- 12 November 2018, pp. 177-183
- Print publication:
- April 2019
-
- Article
-
- You have access
- Export citation
PARITY RESULTS FOR PARTITIONS WHEREIN EACH PART APPEARS AN ODD NUMBER OF TIMES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 99 / Issue 1 / February 2019
- Published online by Cambridge University Press:
- 12 November 2018, pp. 51-55
- Print publication:
- February 2019
-
- Article
-
- You have access
- Export citation
Minimally ramified deformations when
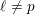 $\ell \neq p$
$\ell \neq p$
- Part of
-
- Journal:
- Compositio Mathematica / Volume 155 / Issue 1 / January 2019
- Published online by Cambridge University Press:
- 12 November 2018, pp. 1-37
- Print publication:
- January 2019
-
- Article
- Export citation
Cyclotomic analogues of finite multiple zeta values
- Part of
-
- Journal:
- Compositio Mathematica / Volume 154 / Issue 12 / December 2018
- Published online by Cambridge University Press:
- 06 November 2018, pp. 2701-2721
- Print publication:
- December 2018
-
- Article
- Export citation
Automorphic vector bundles with global sections on
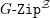 $G\text{-}\mathtt{Zip}^{{\mathcal{Z}}}$-schemes
$G\text{-}\mathtt{Zip}^{{\mathcal{Z}}}$-schemes
- Part of
-
- Journal:
- Compositio Mathematica / Volume 154 / Issue 12 / December 2018
- Published online by Cambridge University Press:
- 31 October 2018, pp. 2586-2605
- Print publication:
- December 2018
-
- Article
- Export citation
ON IWASAWA THEORY OF RUBIN–STARK UNITS AND NARROW CLASS GROUPS
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 61 / Issue 3 / September 2019
- Published online by Cambridge University Press:
- 31 October 2018, pp. 673-691
- Print publication:
- September 2019
-
- Article
-
- You have access
- Export citation
The Quotient Problem for Entire Functions
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 62 / Issue 3 / September 2019
- Published online by Cambridge University Press:
- 26 October 2018, pp. 479-489
- Print publication:
- September 2019
-
- Article
-
- You have access
- Export citation
Consecutive Integers with Close Kernels
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 62 / Issue 3 / September 2019
- Published online by Cambridge University Press:
- 24 October 2018, pp. 469-473
- Print publication:
- September 2019
-
- Article
-
- You have access
- Export citation
RAMANUJAN SERIES WITH A SHIFT
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 107 / Issue 3 / December 2019
- Published online by Cambridge University Press:
- 23 October 2018, pp. 367-380
- Print publication:
- December 2019
-
- Article
-
- You have access
- Export citation
Random ordering in modulus of consecutive Hecke eigenvalues of primitive forms
- Part of
-
- Journal:
- Compositio Mathematica / Volume 154 / Issue 11 / November 2018
- Published online by Cambridge University Press:
- 18 October 2018, pp. 2441-2461
- Print publication:
- November 2018
-
- Article
- Export citation
PRIME SOLUTIONS TO POLYNOMIAL EQUATIONS IN MANY VARIABLES AND DIFFERING DEGREES
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 6 / 2018
- Published online by Cambridge University Press:
- 18 October 2018, e19
-
- Article
-
- You have access
- Open access
- Export citation
Counting fundamental solutions to the Pell equation with prescribed size
- Part of
-
- Journal:
- Compositio Mathematica / Volume 154 / Issue 11 / November 2018
- Published online by Cambridge University Press:
- 11 October 2018, pp. 2379-2402
- Print publication:
- November 2018
-
- Article
- Export citation