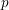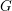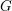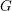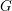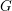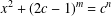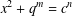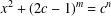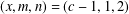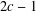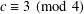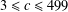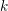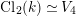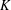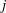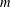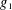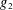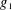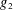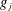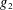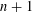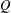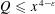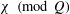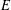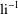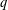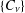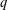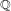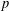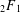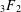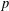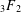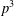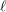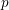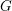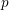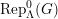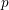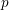Refine listing
Actions for selected content:
2814 results in 11xxx
INTERTWINING SEMISIMPLE CHARACTERS FOR
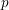 $p$-ADIC CLASSICAL GROUPS
$p$-ADIC CLASSICAL GROUPS
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 238 / June 2020
- Published online by Cambridge University Press:
- 16 July 2018, pp. 137-205
- Print publication:
- June 2020
-
- Article
-
- You have access
- HTML
- Export citation
A SIMPLE PROOF OF CHEBOTAREV’S DENSITY THEOREM OVER FINITE FIELDS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 98 / Issue 2 / October 2018
- Published online by Cambridge University Press:
- 12 July 2018, pp. 196-202
- Print publication:
- October 2018
-
- Article
-
- You have access
- Export citation
A NOTE ON THE DIOPHANTINE EQUATION
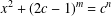 $x^{2}+(2c-1)^{m}=c^{n}$
$x^{2}+(2c-1)^{m}=c^{n}$
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 98 / Issue 2 / October 2018
- Published online by Cambridge University Press:
- 12 July 2018, pp. 188-195
- Print publication:
- October 2018
-
- Article
-
- You have access
- Export citation
DISTRIBUTION OF GALOIS GROUPS OF MAXIMAL UNRAMIFIED 2-EXTENSIONS OVER IMAGINARY QUADRATIC FIELDS
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 237 / March 2020
- Published online by Cambridge University Press:
- 09 July 2018, pp. 166-187
- Print publication:
- March 2020
-
- Article
-
- You have access
- HTML
- Export citation
THE DENSITY OF
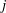 $j$-WISE RELATIVELY
$j$-WISE RELATIVELY  $r$-PRIME ALGEBRAIC INTEGERS
$r$-PRIME ALGEBRAIC INTEGERS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 98 / Issue 2 / October 2018
- Published online by Cambridge University Press:
- 06 July 2018, pp. 221-229
- Print publication:
- October 2018
-
- Article
-
- You have access
- Export citation
ON BINARY CORRELATIONS OF MULTIPLICATIVE FUNCTIONS
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 6 / 2018
- Published online by Cambridge University Press:
- 28 June 2018, e10
-
- Article
-
- You have access
- Open access
- Export citation
Siegel families with application to class fields
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 148 / Issue 4 / August 2018
- Published online by Cambridge University Press:
- 27 June 2018, pp. 751-771
- Print publication:
- August 2018
-
- Article
-
- You have access
- Export citation
Arithmetical Power Series Expansion of the Sigma Function for a Plane Curve
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 61 / Issue 4 / November 2018
- Published online by Cambridge University Press:
- 22 June 2018, pp. 995-1022
-
- Article
- Export citation
On linear independence measures of the values of Mahler functions
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 148 / Issue 6 / December 2018
- Published online by Cambridge University Press:
- 22 June 2018, pp. 1297-1311
- Print publication:
- December 2018
-
- Article
- Export citation
LIFTING N-DIMENSIONAL GALOIS REPRESENTATIONS TO CHARACTERISTIC ZERO
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 61 / Issue 1 / January 2019
- Published online by Cambridge University Press:
- 20 June 2018, pp. 115-150
- Print publication:
- January 2019
-
- Article
-
- You have access
- Export citation
SHIDLOVSKY’S MULTIPLICITY ESTIMATE AND IRRATIONALITY OF ZETA VALUES
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 105 / Issue 2 / October 2018
- Published online by Cambridge University Press:
- 18 June 2018, pp. 145-172
- Print publication:
- October 2018
-
- Article
-
- You have access
- Export citation
AN ARITHMETIC EQUIVALENCE OF THE RIEMANN HYPOTHESIS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 106 / Issue 2 / April 2019
- Published online by Cambridge University Press:
- 18 June 2018, pp. 235-273
- Print publication:
- April 2019
-
- Article
-
- You have access
- Export citation
THETA BLOCK FOURIER EXPANSIONS, BORCHERDS PRODUCTS AND A SEQUENCE OF NEWMAN AND SHANKS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 98 / Issue 1 / August 2018
- Published online by Cambridge University Press:
- 14 June 2018, pp. 48-59
- Print publication:
- August 2018
-
- Article
-
- You have access
- Export citation
DISTINGUISHED MODELS OF INTERMEDIATE JACOBIANS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 19 / Issue 3 / May 2020
- Published online by Cambridge University Press:
- 08 June 2018, pp. 891-918
- Print publication:
- May 2020
-
- Article
- Export citation
INTEGRAL AND ADELIC ASPECTS OF THE MUMFORD–TATE CONJECTURE
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 19 / Issue 3 / May 2020
- Published online by Cambridge University Press:
- 07 June 2018, pp. 869-890
- Print publication:
- May 2020
-
- Article
- Export citation
SUPERCONGRUENCES INVOLVING
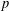 $p$ -ADIC GAMMA FUNCTIONS
$p$ -ADIC GAMMA FUNCTIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 98 / Issue 1 / August 2018
- Published online by Cambridge University Press:
- 30 May 2018, pp. 27-37
- Print publication:
- August 2018
-
- Article
-
- You have access
- Export citation
Sur les
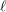 $\ell$ -blocs de niveau zéro des groupes
$\ell$ -blocs de niveau zéro des groupes 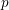 $p$ -adiques
$p$ -adiques
- Part of
-
- Journal:
- Compositio Mathematica / Volume 154 / Issue 7 / July 2018
- Published online by Cambridge University Press:
- 24 May 2018, pp. 1473-1507
- Print publication:
- July 2018
-
- Article
- Export citation
RANKIN–SELBERG CONVOLUTIONS OF NONCUSPIDAL HALF-INTEGRAL WEIGHT MAASS FORMS IN THE PLUS SPACE
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 237 / March 2020
- Published online by Cambridge University Press:
- 21 May 2018, pp. 127-165
- Print publication:
- March 2020
-
- Article
-
- You have access
- HTML
- Export citation
Arithmetic intersection on GSpin Rapoport–Zink spaces
- Part of
-
- Journal:
- Compositio Mathematica / Volume 154 / Issue 7 / July 2018
- Published online by Cambridge University Press:
- 16 May 2018, pp. 1407-1440
- Print publication:
- July 2018
-
- Article
- Export citation
Duality for relative logarithmic de Rham–Witt sheaves and wildly ramified class field theory over finite fields
- Part of
-
- Journal:
- Compositio Mathematica / Volume 154 / Issue 6 / June 2018
- Published online by Cambridge University Press:
- 07 May 2018, pp. 1306-1331
- Print publication:
- June 2018
-
- Article
- Export citation