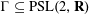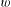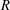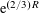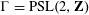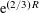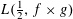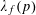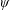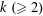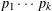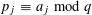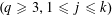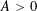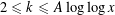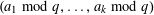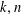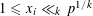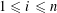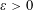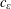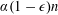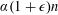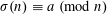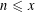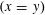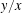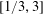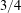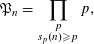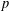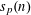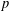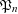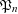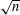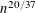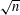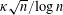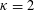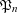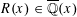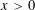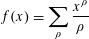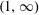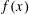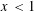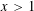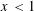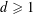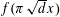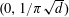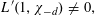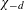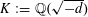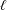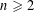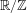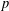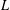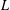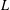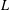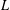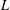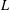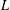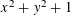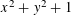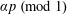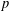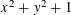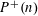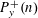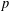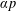Refine listing
Actions for selected content:
2816 results in 11xxx
LOCAL AVERAGE OF THE HYPERBOLIC CIRCLE PROBLEM FOR FUCHSIAN GROUPS
- Part of
-
- Journal:
- Mathematika / Volume 64 / Issue 1 / 2018
- Published online by Cambridge University Press:
- 06 February 2018, pp. 159-183
- Print publication:
- 2018
-
- Article
- Export citation
LEVEL RECIPROCITY IN THE TWISTED SECOND MOMENT OF RANKIN–SELBERG
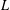 $L$-FUNCTIONS
$L$-FUNCTIONS
- Part of
-
- Journal:
- Mathematika / Volume 64 / Issue 3 / 2018
- Published online by Cambridge University Press:
- 26 June 2018, pp. 770-784
- Print publication:
- 2018
-
- Article
- Export citation
HAUSDORFF MEASURE OF SETS OF DIRICHLET NON-IMPROVABLE NUMBERS
- Part of
-
- Journal:
- Mathematika / Volume 64 / Issue 2 / 2018
- Published online by Cambridge University Press:
- 19 April 2018, pp. 502-518
- Print publication:
- 2018
-
- Article
- Export citation
LARGE BIAS FOR INTEGERS WITH PRIME FACTORS IN ARITHMETIC PROGRESSIONS
- Part of
-
- Journal:
- Mathematika / Volume 64 / Issue 1 / 2018
- Published online by Cambridge University Press:
- 15 February 2018, pp. 237-252
- Print publication:
- 2018
-
- Article
- Export citation
SOLUTIONS TO DIAGONAL CONGRUENCES WITH VARIABLES RESTRICTED TO A BOX
- Part of
-
- Journal:
- Mathematika / Volume 64 / Issue 2 / 2018
- Published online by Cambridge University Press:
- 03 April 2018, pp. 430-444
- Print publication:
- 2018
-
- Article
- Export citation
DIVISOR-SUM FIBERS
- Part of
-
- Journal:
- Mathematika / Volume 64 / Issue 2 / 2018
- Published online by Cambridge University Press:
- 03 April 2018, pp. 330-342
- Print publication:
- 2018
-
- Article
- Export citation
ALGEBRAIC TORI AS DEGENERATIONS OF ABELIAN VARIETIES
- Part of
-
- Journal:
- Mathematika / Volume 64 / Issue 2 / 2018
- Published online by Cambridge University Press:
- 20 March 2018, pp. 303-329
- Print publication:
- 2018
-
- Article
-
- You have access
- HTML
- Export citation
TRIANGLES CAPTURING MANY LATTICE POINTS
- Part of
-
- Journal:
- Mathematika / Volume 64 / Issue 2 / 2018
- Published online by Cambridge University Press:
- 25 April 2018, pp. 551-582
- Print publication:
- 2018
-
- Article
- Export citation
DENOMINATORS OF BERNOULLI POLYNOMIALS
- Part of
-
- Journal:
- Mathematika / Volume 64 / Issue 2 / 2018
- Published online by Cambridge University Press:
- 16 April 2018, pp. 519-541
- Print publication:
- 2018
-
- Article
- Export citation
A METRIC THEORY OF MINIMAL GAPS
- Part of
-
- Journal:
- Mathematika / Volume 64 / Issue 3 / 2018
- Published online by Cambridge University Press:
- 21 May 2018, pp. 628-636
- Print publication:
- 2018
-
- Article
- Export citation
TRANSCENDENTAL SUMS RELATED TO THE ZEROS OF ZETA FUNCTIONS
- Part of
-
- Journal:
- Mathematika / Volume 64 / Issue 3 / 2018
- Published online by Cambridge University Press:
- 01 August 2018, pp. 875-897
- Print publication:
- 2018
-
- Article
- Export citation
INTEGRAL MONODROMY GROUPS OF KLOOSTERMAN SHEAVES
- Part of
-
- Journal:
- Mathematika / Volume 64 / Issue 3 / 2018
- Published online by Cambridge University Press:
- 08 June 2018, pp. 652-678
- Print publication:
- 2018
-
- Article
- Export citation
WEAK ADMISSIBILITY, PRIMITIVITY, O-MINIMALITY, AND DIOPHANTINE APPROXIMATION
- Part of
-
- Journal:
- Mathematika / Volume 64 / Issue 2 / 2018
- Published online by Cambridge University Press:
- 17 April 2018, pp. 475-496
- Print publication:
- 2018
-
- Article
- Export citation
THE PRIMES ARE NOT METRIC POISSONIAN
- Part of
-
- Journal:
- Mathematika / Volume 64 / Issue 1 / 2018
- Published online by Cambridge University Press:
- 14 February 2018, pp. 230-236
- Print publication:
- 2018
-
- Article
- Export citation
TRUNCATED PRODUCT REPRESENTATIONS FOR
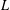 $L$ -FUNCTIONS IN THE HYPERELLIPTIC ENSEMBLE
$L$ -FUNCTIONS IN THE HYPERELLIPTIC ENSEMBLE
- Part of
-
- Journal:
- Mathematika / Volume 64 / Issue 1 / 2018
- Published online by Cambridge University Press:
- 06 February 2018, pp. 137-158
- Print publication:
- 2018
-
- Article
- Export citation
ADDITIVE ENERGY AND THE METRIC POISSONIAN PROPERTY
- Part of
-
- Journal:
- Mathematika / Volume 64 / Issue 3 / 2018
- Published online by Cambridge University Press:
- 19 June 2018, pp. 679-700
- Print publication:
- 2018
-
- Article
- Export citation
THE GOLDBACH PROBLEM FOR PRIMES THAT ARE SUMS OF TWO SQUARES PLUS ONE
- Part of
-
- Journal:
- Mathematika / Volume 64 / Issue 1 / 2018
- Published online by Cambridge University Press:
- 25 January 2018, pp. 20-70
- Print publication:
- 2018
-
- Article
- Export citation
SUR LES PLUS GRANDS FACTEURS PREMIERSD’ENTIERS CONSÉCUTIFS
- Part of
-
- Journal:
- Mathematika / Volume 64 / Issue 2 / 2018
- Published online by Cambridge University Press:
- 05 April 2018, pp. 343-379
- Print publication:
- 2018
-
- Article
- Export citation
TERNARY DIVISOR FUNCTIONS IN ARITHMETIC PROGRESSIONS TO SMOOTH MODULI
- Part of
-
- Journal:
- Mathematika / Volume 64 / Issue 3 / 2018
- Published online by Cambridge University Press:
- 19 June 2018, pp. 701-729
- Print publication:
- 2018
-
- Article
- Export citation
FRACTIONAL PARTS OF POLYNOMIALS OVER THE PRIMES. II
- Part of
-
- Journal:
- Mathematika / Volume 64 / Issue 3 / 2018
- Published online by Cambridge University Press:
- 26 June 2018, pp. 742-769
- Print publication:
- 2018
-
- Article
- Export citation