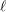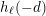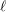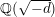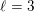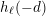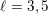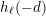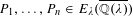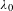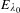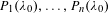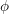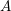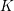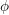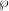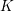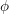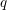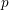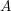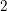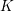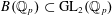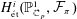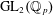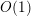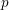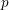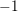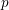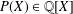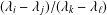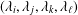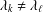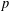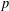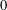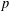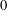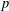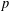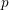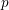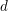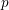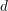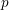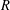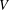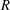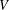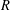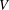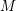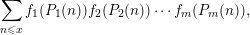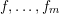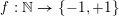Refine listing
Actions for selected content:
2816 results in 11xxx
Averages and moments associated to class numbers of imaginary quadratic fields
- Part of
-
- Journal:
- Compositio Mathematica / Volume 153 / Issue 11 / November 2017
- Published online by Cambridge University Press:
- 14 August 2017, pp. 2287-2309
- Print publication:
- November 2017
-
- Article
-
- You have access
- HTML
- Export citation
Log-concavity and strong q-log-convexity for Riordan arrays and recursive matrices
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 147 / Issue 6 / December 2017
- Published online by Cambridge University Press:
- 14 August 2017, pp. 1297-1310
- Print publication:
- December 2017
-
- Article
-
- You have access
- Export citation
CM RELATIONS IN FIBERED POWERS OF ELLIPTIC FAMILIES
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 18 / Issue 5 / September 2019
- Published online by Cambridge University Press:
- 02 August 2017, pp. 941-956
- Print publication:
- September 2019
-
- Article
- Export citation
Fast Evaluation of the Caputo Fractional Derivative and its Applications to Fractional Diffusion Equations: A Second-Order Scheme
- Part of
- Partial differential equations, initial value and time-dependent initial-boundary value problems
- General theory in ordinary differential equations
- Real functions
- Computational aspects
- Miscellaneous topics - Partial differential equations
- Finite fields and commutative rings (number-theoretic aspects)
-
- Journal:
- Communications in Computational Physics / Volume 22 / Issue 4 / October 2017
- Published online by Cambridge University Press:
- 28 July 2017, pp. 1028-1048
- Print publication:
- October 2017
-
- Article
- Export citation
EXPLICIT SURJECTIVITY RESULTS FOR DRINFELD MODULES OF RANK 2
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 234 / June 2019
- Published online by Cambridge University Press:
- 27 July 2017, pp. 17-45
- Print publication:
- June 2019
-
- Article
-
- You have access
- HTML
- Export citation
A QUOTIENT OF THE LUBIN–TATE TOWER
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 5 / 2017
- Published online by Cambridge University Press:
- 27 July 2017, e17
-
- Article
-
- You have access
- Open access
- Export citation
The Pila–Wilkie theorem for subanalytic families: a complex analytic approach
- Part of
-
- Journal:
- Compositio Mathematica / Volume 153 / Issue 10 / October 2017
- Published online by Cambridge University Press:
- 27 July 2017, pp. 2171-2194
- Print publication:
- October 2017
-
- Article
- Export citation
The
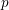 $p$ -adic Gross–Zagier formula on Shimura curves
$p$ -adic Gross–Zagier formula on Shimura curves
- Part of
-
- Journal:
- Compositio Mathematica / Volume 153 / Issue 10 / October 2017
- Published online by Cambridge University Press:
- 11 July 2017, pp. 1987-2074
- Print publication:
- October 2017
-
- Article
- Export citation
ON POLYNOMIALS WHOSE ROOTS HAVE RATIONAL QUOTIENT OF DIFFERENCES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 96 / Issue 2 / October 2017
- Published online by Cambridge University Press:
- 05 July 2017, pp. 185-190
- Print publication:
- October 2017
-
- Article
-
- You have access
- Export citation
WHITTAKER FUNCTIONS AND DEMAZURE CHARACTERS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 18 / Issue 4 / July 2019
- Published online by Cambridge University Press:
- 22 June 2017, pp. 759-781
- Print publication:
- July 2019
-
- Article
- Export citation
Explicit Serre weights for two-dimensional Galois representations
- Part of
-
- Journal:
- Compositio Mathematica / Volume 153 / Issue 9 / September 2017
- Published online by Cambridge University Press:
- 20 June 2017, pp. 1893-1907
- Print publication:
- September 2017
-
- Article
- Export citation
Automorphic products of singular weight
- Part of
-
- Journal:
- Compositio Mathematica / Volume 153 / Issue 9 / September 2017
- Published online by Cambridge University Press:
- 20 June 2017, pp. 1855-1892
- Print publication:
- September 2017
-
- Article
- Export citation
TRANSPORT PARALLÈLE ET CORRESPONDANCE DE SIMPSON
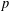 $p$ -ADIQUE
$p$ -ADIQUE
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 5 / 2017
- Published online by Cambridge University Press:
- 19 June 2017, e13
-
- Article
-
- You have access
- Open access
- Export citation
Minimal weights of Hilbert modular forms in characteristic
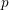 $p$
$p$
- Part of
-
- Journal:
- Compositio Mathematica / Volume 153 / Issue 9 / September 2017
- Published online by Cambridge University Press:
- 13 June 2017, pp. 1769-1778
- Print publication:
- September 2017
-
- Article
- Export citation
A NOTE ON SCHMIDT’S CONJECTURE
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 96 / Issue 2 / October 2017
- Published online by Cambridge University Press:
- 09 June 2017, pp. 191-195
- Print publication:
- October 2017
-
- Article
-
- You have access
- Export citation
CONGRUENCE OF SYMMETRIC INNER PRODUCTS OVER FINITE COMMUTATIVE RINGS OF ODD CHARACTERISTIC
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 96 / Issue 3 / December 2017
- Published online by Cambridge University Press:
- 08 June 2017, pp. 389-397
- Print publication:
- December 2017
-
- Article
-
- You have access
- Export citation
Construction of automorphisms of hyperkähler manifolds
- Part of
-
- Journal:
- Compositio Mathematica / Volume 153 / Issue 8 / August 2017
- Published online by Cambridge University Press:
- 31 May 2017, pp. 1610-1621
- Print publication:
- August 2017
-
- Article
- Export citation
Correlations of multiplicative functions and applications
- Part of
-
- Journal:
- Compositio Mathematica / Volume 153 / Issue 8 / August 2017
- Published online by Cambridge University Press:
- 31 May 2017, pp. 1622-1657
- Print publication:
- August 2017
-
- Article
- Export citation
COMPETITIVE ANALYSIS OF INTERRELATED PRICE ONLINE INVENTORY PROBLEMS WITH DEMANDS
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 58 / Issue 3-4 / April 2017
- Published online by Cambridge University Press:
- 15 May 2017, pp. 368-378
-
- Article
-
- You have access
- Export citation
Non-abelian Cohen–Lenstra heuristics over function fields
- Part of
-
- Journal:
- Compositio Mathematica / Volume 153 / Issue 7 / July 2017
- Published online by Cambridge University Press:
- 12 May 2017, pp. 1372-1390
- Print publication:
- July 2017
-
- Article
- Export citation