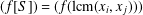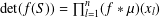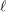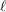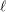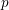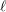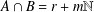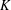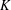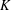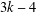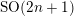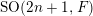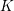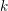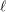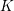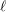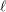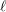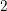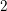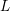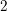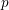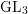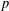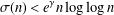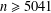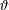Refine listing
Actions for selected content:
2818 results in 11xxx
Arithmetic properties of Apéry-like numbers
- Part of
-
- Journal:
- Compositio Mathematica / Volume 154 / Issue 2 / February 2018
- Published online by Cambridge University Press:
- 20 October 2017, pp. 249-274
- Print publication:
- February 2018
-
- Article
- Export citation
MORE ON A CERTAIN ARITHMETICAL DETERMINANT
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 97 / Issue 1 / February 2018
- Published online by Cambridge University Press:
- 17 October 2017, pp. 15-25
- Print publication:
- February 2018
-
- Article
-
- You have access
- Export citation
Around
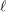 $\ell$ -independence
$\ell$ -independence
- Part of
-
- Journal:
- Compositio Mathematica / Volume 154 / Issue 1 / January 2018
- Published online by Cambridge University Press:
- 17 October 2017, pp. 223-248
- Print publication:
- January 2018
-
- Article
- Export citation
Rational points on hyperelliptic curves having a marked non-Weierstrass point
- Part of
-
- Journal:
- Compositio Mathematica / Volume 154 / Issue 1 / January 2018
- Published online by Cambridge University Press:
- 09 October 2017, pp. 188-222
- Print publication:
- January 2018
-
- Article
- Export citation
Nearby cycles of automorphic étale sheaves
- Part of
-
- Journal:
- Compositio Mathematica / Volume 154 / Issue 1 / January 2018
- Published online by Cambridge University Press:
- 05 October 2017, pp. 80-119
- Print publication:
- January 2018
-
- Article
- Export citation
NOTE ON LEHMER–PIERCE SEQUENCES WITH THE SAME PRIME DIVISORS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 97 / Issue 1 / February 2018
- Published online by Cambridge University Press:
- 04 October 2017, pp. 11-14
- Print publication:
- February 2018
-
- Article
-
- You have access
- Export citation
PARTITIONS OF THE SET OF NONNEGATIVE INTEGERS WITH THE SAME REPRESENTATION FUNCTIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 97 / Issue 2 / April 2018
- Published online by Cambridge University Press:
- 04 October 2017, pp. 200-206
- Print publication:
- April 2018
-
- Article
-
- You have access
- Export citation
ON PERFECT
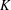 $K$ -RATIONAL CUBOIDS
$K$ -RATIONAL CUBOIDS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 97 / Issue 1 / February 2018
- Published online by Cambridge University Press:
- 04 October 2017, pp. 26-32
- Print publication:
- February 2018
-
- Article
-
- You have access
- Export citation
The Schwarzian equation for completely replicable functions
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 20 / Issue 1 / 2017
- Published online by Cambridge University Press:
- 01 October 2017, pp. 30-52
-
- Article
-
- You have access
- Export citation
THE
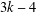 $3k-4$ THEOREM FOR ORDERED GROUPS
$3k-4$ THEOREM FOR ORDERED GROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 97 / Issue 1 / February 2018
- Published online by Cambridge University Press:
- 28 September 2017, pp. 43-46
- Print publication:
- February 2018
-
- Article
-
- You have access
- Export citation
REPRÉSENTATIONS DE RÉDUCTION UNIPOTENTE POUR
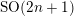 $\operatorname{SO}(2n+1)$, II : ENDOSCOPIE
$\operatorname{SO}(2n+1)$, II : ENDOSCOPIE
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 233 / March 2019
- Published online by Cambridge University Press:
- 21 September 2017, pp. 87-154
- Print publication:
- March 2019
-
- Article
-
- You have access
- HTML
- Export citation
CM FIELDS WITHOUT UNIT-PRIMITIVE ELEMENTS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 96 / Issue 3 / December 2017
- Published online by Cambridge University Press:
- 20 September 2017, pp. 398-399
- Print publication:
- December 2017
-
- Article
-
- You have access
- Export citation
Good reduction of K3 surfaces
- Part of
-
- Journal:
- Compositio Mathematica / Volume 154 / Issue 1 / January 2018
- Published online by Cambridge University Press:
- 18 September 2017, pp. 1-35
- Print publication:
- January 2018
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
TEST VECTORS FOR LOCAL CUSPIDAL RANKIN–SELBERG INTEGRALS
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 233 / March 2019
- Published online by Cambridge University Press:
- 12 September 2017, pp. 170-192
- Print publication:
- March 2019
-
- Article
-
- You have access
- HTML
- Export citation
Bad reduction of genus
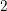 $2$ curves with CM jacobian varieties
$2$ curves with CM jacobian varieties
- Part of
-
- Journal:
- Compositio Mathematica / Volume 153 / Issue 12 / December 2017
- Published online by Cambridge University Press:
- 11 September 2017, pp. 2534-2576
- Print publication:
- December 2017
-
- Article
- Export citation
On mod
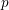 $p$ local-global compatibility for
$p$ local-global compatibility for 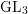 $\text{GL}_{3}$ in the ordinary case
$\text{GL}_{3}$ in the ordinary case
- Part of
-
- Journal:
- Compositio Mathematica / Volume 153 / Issue 11 / November 2017
- Published online by Cambridge University Press:
- 25 August 2017, pp. 2215-2286
- Print publication:
- November 2017
-
- Article
- Export citation
ON THE MINIMAL NUMBER OF SMALL ELEMENTS GENERATING FINITE PRIME FIELDS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 96 / Issue 2 / October 2017
- Published online by Cambridge University Press:
- 17 August 2017, pp. 177-184
- Print publication:
- October 2017
-
- Article
-
- You have access
- Export citation
SYMMETRIC SQUARE-CENTRAL ELEMENTS IN PRODUCTS OF ORTHOGONAL INVOLUTIONS IN CHARACTERISTIC TWO
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 96 / Issue 3 / December 2017
- Published online by Cambridge University Press:
- 17 August 2017, pp. 412-425
- Print publication:
- December 2017
-
- Article
-
- You have access
- Export citation
RAMIFICATION IN KUMMER EXTENSIONS ARISING FROM ALGEBRAIC TORI
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 96 / Issue 2 / October 2017
- Published online by Cambridge University Press:
- 17 August 2017, pp. 196-204
- Print publication:
- October 2017
-
- Article
-
- You have access
- Export citation
A NEW UPPER BOUND FOR THE SUM OF DIVISORS FUNCTION
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 96 / Issue 3 / December 2017
- Published online by Cambridge University Press:
- 14 August 2017, pp. 374-379
- Print publication:
- December 2017
-
- Article
-
- You have access
- Export citation