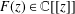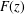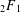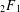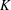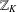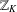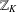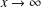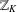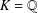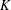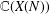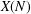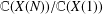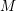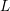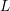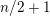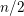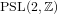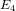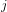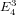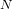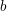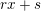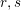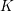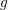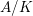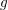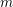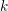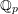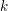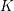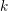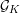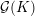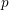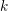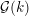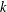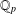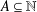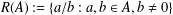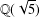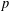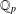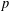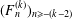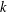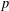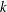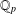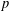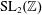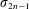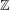Refine listing
Actions for selected content:
2816 results in 11xxx
TRANSCENDENCE OVER MEROMORPHIC FUNCTIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 95 / Issue 3 / June 2017
- Published online by Cambridge University Press:
- 13 March 2017, pp. 393-399
- Print publication:
- June 2017
-
- Article
-
- You have access
- Export citation
CONGRUENCES FOR TRUNCATED HYPERGEOMETRIC SERIES
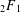 $_{2}F_{1}$
$_{2}F_{1}$
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 96 / Issue 1 / August 2017
- Published online by Cambridge University Press:
- 06 March 2017, pp. 14-23
- Print publication:
- August 2017
-
- Article
-
- You have access
- Export citation
TWO PROBLEMS CONCERNING IRREDUCIBLE ELEMENTS IN RINGS OF INTEGERS OF NUMBER FIELDS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 96 / Issue 1 / August 2017
- Published online by Cambridge University Press:
- 02 March 2017, pp. 44-58
- Print publication:
- August 2017
-
- Article
-
- You have access
- Export citation
NORMAL BASES FOR MODULAR FUNCTION FIELDS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 95 / Issue 3 / June 2017
- Published online by Cambridge University Press:
- 02 March 2017, pp. 384-392
- Print publication:
- June 2017
-
- Article
-
- You have access
- Export citation
ON THE TENTH-ORDER MOCK THETA FUNCTIONS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 104 / Issue 1 / February 2018
- Published online by Cambridge University Press:
- 02 March 2017, pp. 44-62
- Print publication:
- February 2018
-
- Article
-
- You have access
- Export citation
Spinors and essential dimension
- Part of
-
- Journal:
- Compositio Mathematica / Volume 153 / Issue 3 / March 2017
- Published online by Cambridge University Press:
- 02 March 2017, pp. 535-556
- Print publication:
- March 2017
-
- Article
- Export citation
Height pairings on orthogonal Shimura varieties
- Part of
-
- Journal:
- Compositio Mathematica / Volume 153 / Issue 3 / March 2017
- Published online by Cambridge University Press:
- 02 March 2017, pp. 474-534
- Print publication:
- March 2017
-
- Article
- Export citation
Picard curves over
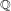 $\mathbb{Q}$ with good reduction away from 3
$\mathbb{Q}$ with good reduction away from 3
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 19 / Issue 2 / 2016
- Published online by Cambridge University Press:
- 01 March 2017, pp. 382-408
-
- Article
-
- You have access
- Export citation
Certain aspects of holomorphic function theory on some genus-zero arithmetic groups
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 19 / Issue 2 / 2016
- Published online by Cambridge University Press:
- 01 March 2017, pp. 360-381
-
- Article
-
- You have access
- Export citation
Geometric-progression-free sets over quadratic number fields
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 147 / Issue 2 / April 2017
- Published online by Cambridge University Press:
- 27 February 2017, pp. 245-262
- Print publication:
- April 2017
-
- Article
- Export citation
Une nouvelle approche dans la théorie des entiers friables
- Part of
-
- Journal:
- Compositio Mathematica / Volume 153 / Issue 3 / March 2017
- Published online by Cambridge University Press:
- 20 February 2017, pp. 453-473
- Print publication:
- March 2017
-
- Article
- Export citation
EXPLICIT ZERO-COUNTING THEOREM FOR HECKE–LANDAU ZETA-FUNCTIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 95 / Issue 3 / June 2017
- Published online by Cambridge University Press:
- 06 February 2017, pp. 400-411
- Print publication:
- June 2017
-
- Article
-
- You have access
- Export citation
Commensurability of automorphism groups
- Part of
-
- Journal:
- Compositio Mathematica / Volume 153 / Issue 2 / February 2017
- Published online by Cambridge University Press:
- 06 February 2017, pp. 323-346
- Print publication:
- February 2017
-
- Article
- Export citation
Non-trivial matrix actions preserve normality for continued fractions
- Part of
-
- Journal:
- Compositio Mathematica / Volume 153 / Issue 2 / February 2017
- Published online by Cambridge University Press:
- 06 February 2017, pp. 274-293
- Print publication:
- February 2017
-
- Article
- Export citation
Level structures on abelian varieties and Vojta’s conjecture
- Part of
-
- Journal:
- Compositio Mathematica / Volume 153 / Issue 2 / February 2017
- Published online by Cambridge University Press:
- 06 February 2017, pp. 373-394
- Print publication:
- February 2017
-
- Article
- Export citation
Stable vectors in Moy–Prasad filtrations
- Part of
-
- Journal:
- Compositio Mathematica / Volume 153 / Issue 2 / February 2017
- Published online by Cambridge University Press:
- 09 February 2017, pp. 358-372
- Print publication:
- February 2017
-
- Article
- Export citation
A Generalization of the Eisenstein–Dumas–Schönemann Irreducibility Criterion
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 60 / Issue 4 / November 2017
- Published online by Cambridge University Press:
- 31 January 2017, pp. 937-945
-
- Article
- Export citation
MONOTONIC PHINOMIAL COEFFICIENTS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 95 / Issue 3 / June 2017
- Published online by Cambridge University Press:
- 09 January 2017, pp. 365-372
- Print publication:
- June 2017
-
- Article
-
- You have access
- Export citation
THE QUOTIENT SET OF
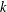 $k$ -GENERALISED FIBONACCI NUMBERS IS DENSE IN
$k$ -GENERALISED FIBONACCI NUMBERS IS DENSE IN 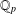 $\mathbb{Q}_{p}$
$\mathbb{Q}_{p}$
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 96 / Issue 1 / August 2017
- Published online by Cambridge University Press:
- 09 January 2017, pp. 24-29
- Print publication:
- August 2017
-
- Article
-
- You have access
- Export citation
ZETA ELEMENTS IN DEPTH 3 AND THE FUNDAMENTAL LIE ALGEBRA OF THE INFINITESIMAL TATE CURVE
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 5 / 2017
- Published online by Cambridge University Press:
- 05 January 2017, e1
-
- Article
-
- You have access
- Open access
- Export citation