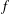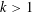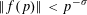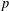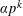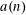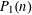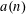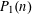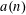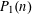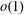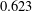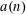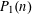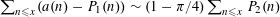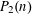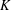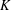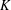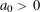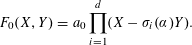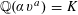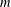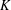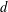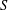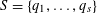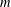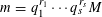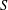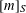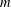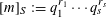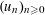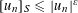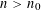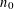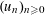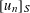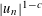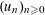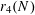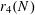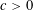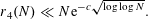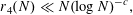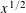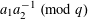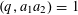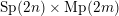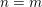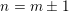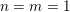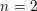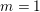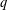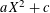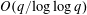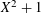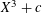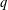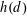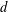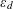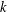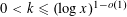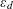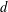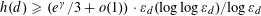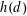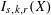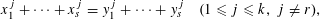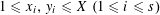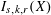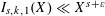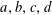Refine listing
Actions for selected content:
2816 results in 11xxx
POINT DISTRIBUTIONS IN COMPACT METRIC SPACES
- Part of
-
- Journal:
- Mathematika / Volume 63 / Issue 3 / 2017
- Published online by Cambridge University Press:
- 29 November 2017, pp. 1152-1171
- Print publication:
- 2017
-
- Article
- Export citation
ABCOLOGICAL ANECDOTES
- Part of
-
- Journal:
- Mathematika / Volume 63 / Issue 3 / 2017
- Published online by Cambridge University Press:
- 29 November 2017, pp. 713-714
- Print publication:
- 2017
-
- Article
- Export citation
PARAMETRIC GEOMETRY OF NUMBERS IN FUNCTION FIELDS
- Part of
-
- Journal:
- Mathematika / Volume 63 / Issue 3 / 2017
- Published online by Cambridge University Press:
- 29 November 2017, pp. 1114-1135
- Print publication:
- 2017
-
- Article
- Export citation
FRACTIONAL PARTS OF POLYNOMIALS OVER THE PRIMES
- Part of
-
- Journal:
- Mathematika / Volume 63 / Issue 3 / 2017
- Published online by Cambridge University Press:
- 29 November 2017, pp. 715-733
- Print publication:
- 2017
-
- Article
- Export citation
RANDOM MULTIPLICATIVE WALKS ON THE RESIDUES MODULO
 $n$
$n$
- Part of
-
- Journal:
- Mathematika / Volume 63 / Issue 2 / 2017
- Published online by Cambridge University Press:
- 12 May 2017, pp. 602-621
- Print publication:
- 2017
-
- Article
- Export citation
MANY CUBIC SURFACES CONTAIN RATIONAL POINTS
- Part of
-
- Journal:
- Mathematika / Volume 63 / Issue 3 / 2017
- Published online by Cambridge University Press:
- 29 November 2017, pp. 818-839
- Print publication:
- 2017
-
- Article
- Export citation
FAMILIES OF THUE EQUATIONS ASSOCIATED WITH A RANK ONE SUBGROUP OF THE UNIT GROUP OF A NUMBER FIELD
- Part of
-
- Journal:
- Mathematika / Volume 63 / Issue 3 / 2017
- Published online by Cambridge University Press:
- 29 November 2017, pp. 1060-1080
- Print publication:
- 2017
-
- Article
- Export citation
PRIMES AND PRIME IDEALS IN SHORT INTERVALS
- Part of
-
- Journal:
- Mathematika / Volume 63 / Issue 2 / 2017
- Published online by Cambridge University Press:
- 09 February 2017, pp. 364-371
- Print publication:
- 2017
-
- Article
-
- You have access
- HTML
- Export citation
 $S$ -PARTS OF TERMS OF INTEGER LINEAR RECURRENCE SEQUENCES
$S$ -PARTS OF TERMS OF INTEGER LINEAR RECURRENCE SEQUENCES
- Part of
-
- Journal:
- Mathematika / Volume 63 / Issue 3 / 2017
- Published online by Cambridge University Press:
- 29 November 2017, pp. 840-851
- Print publication:
- 2017
-
- Article
- Export citation
NEW BOUNDS FOR SZEMERÉDI’S THEOREM, III: A POLYLOGARITHMIC BOUND FOR
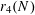 $r_{4}(N)$
$r_{4}(N)$
- Part of
-
- Journal:
- Mathematika / Volume 63 / Issue 3 / 2017
- Published online by Cambridge University Press:
- 29 November 2017, pp. 944-1040
- Print publication:
- 2017
-
- Article
-
- You have access
- HTML
- Export citation
SMOOTH-SUPPORTED MULTIPLICATIVE FUNCTIONS IN ARITHMETIC PROGRESSIONS BEYOND THE
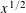 $x^{1/2}$ -BARRIER
$x^{1/2}$ -BARRIER
- Part of
-
- Journal:
- Mathematika / Volume 63 / Issue 3 / 2017
- Published online by Cambridge University Press:
- 29 November 2017, pp. 895-918
- Print publication:
- 2017
-
- Article
- Export citation
Refined global Gan–Gross–Prasad conjecture for Fourier–Jacobi periods on symplectic groups
- Part of
-
- Journal:
- Compositio Mathematica / Volume 153 / Issue 1 / January 2017
- Published online by Cambridge University Press:
- 19 January 2017, pp. 68-131
- Print publication:
- January 2017
-
- Article
- Export citation
RATIONAL POINTS ON THE INNER PRODUCT CONE VIA THE HYPERBOLA METHOD
- Part of
-
- Journal:
- Mathematika / Volume 63 / Issue 3 / 2017
- Published online by Cambridge University Press:
- 29 November 2017, pp. 780-796
- Print publication:
- 2017
-
- Article
- Export citation
ITERATION OF QUADRATIC POLYNOMIALS OVER FINITE FIELDS
- Part of
-
- Journal:
- Mathematika / Volume 63 / Issue 3 / 2017
- Published online by Cambridge University Press:
- 29 November 2017, pp. 1041-1059
- Print publication:
- 2017
-
- Article
- Export citation
Equations of hyperelliptic Shimura curves
- Part of
-
- Journal:
- Compositio Mathematica / Volume 153 / Issue 1 / January 2017
- Published online by Cambridge University Press:
- 19 January 2017, pp. 1-40
- Print publication:
- January 2017
-
- Article
- Export citation
LARGE MOMENTS AND EXTREME VALUES OF CLASS NUMBERS OF INDEFINITE BINARY QUADRATIC FORMS
- Part of
-
- Journal:
- Mathematika / Volume 63 / Issue 2 / 2017
- Published online by Cambridge University Press:
- 20 April 2017, pp. 564-586
- Print publication:
- 2017
-
- Article
- Export citation
VINOGRADOV SYSTEMS WITH A SLICE OFF
- Part of
-
- Journal:
- Mathematika / Volume 63 / Issue 3 / 2017
- Published online by Cambridge University Press:
- 29 November 2017, pp. 797-817
- Print publication:
- 2017
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A NOTE ON BADLY APPROXIMABLE LINEAR FORMS ON MANIFOLDS
- Part of
-
- Journal:
- Mathematika / Volume 63 / Issue 2 / 2017
- Published online by Cambridge University Press:
- 11 May 2017, pp. 587-601
- Print publication:
- 2017
-
- Article
-
- You have access
- HTML
- Export citation
ON THE LEAST SQUAREFREE NUMBER INAN ARITHMETIC PROGRESSION
- Part of
-
- Journal:
- Mathematika / Volume 63 / Issue 2 / 2017
- Published online by Cambridge University Press:
- 23 March 2017, pp. 483-498
- Print publication:
- 2017
-
- Article
- Export citation
ON SOME MULTIPLE CHARACTER SUMS
- Part of
-
- Journal:
- Mathematika / Volume 63 / Issue 2 / 2017
- Published online by Cambridge University Press:
- 03 April 2017, pp. 553-560
- Print publication:
- 2017
-
- Article
- Export citation