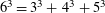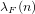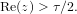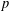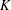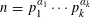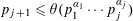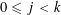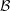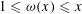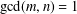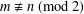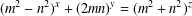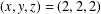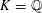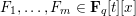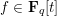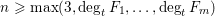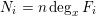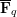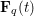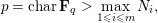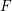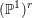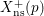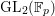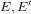Refine listing
Actions for selected content:
2818 results in 11xxx
PERFECT POWERS THAT ARE SUMS OF CONSECUTIVE CUBES
- Part of
-
- Journal:
- Mathematika / Volume 63 / Issue 1 / 2017
- Published online by Cambridge University Press:
- 05 October 2016, pp. 230-249
- Print publication:
- 2017
-
- Article
- Export citation
On a Li-type criterion for zero-free regions of certain Dirichlet series with real coefficients
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 19 / Issue 1 / 2016
- Published online by Cambridge University Press:
- 01 October 2016, pp. 259-280
-
- Article
-
- You have access
- Export citation
ON SELMER RANK PARITY OF TWISTS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 102 / Issue 3 / June 2017
- Published online by Cambridge University Press:
- 28 September 2016, pp. 316-330
- Print publication:
- June 2017
-
- Article
-
- You have access
- Export citation
Local models for Weil-restricted groups
- Part of
-
- Journal:
- Compositio Mathematica / Volume 152 / Issue 12 / December 2016
- Published online by Cambridge University Press:
- 27 September 2016, pp. 2563-2601
- Print publication:
- December 2016
-
- Article
- Export citation
A SIEVE PROBLEM AND ITS APPLICATION
- Part of
-
- Journal:
- Mathematika / Volume 63 / Issue 1 / 2017
- Published online by Cambridge University Press:
- 27 September 2016, pp. 213-229
- Print publication:
- 2017
-
- Article
- Export citation
THE LOGARITHMICALLY AVERAGED CHOWLA AND ELLIOTT CONJECTURES FOR TWO-POINT CORRELATIONS
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 4 / 2016
- Published online by Cambridge University Press:
- 27 September 2016, e8
-
- Article
-
- You have access
- Open access
- Export citation
SHIFTED MOMENTS OF
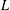 $L$ -FUNCTIONS ANDMOMENTS OF THETA FUNCTIONS
$L$ -FUNCTIONS ANDMOMENTS OF THETA FUNCTIONS
- Part of
-
- Journal:
- Mathematika / Volume 63 / Issue 1 / 2017
- Published online by Cambridge University Press:
- 27 September 2016, pp. 196-212
- Print publication:
- 2017
-
- Article
- Export citation
A NOTE ON JEŚMANOWICZ’ CONJECTURE CONCERNING PRIMITIVE PYTHAGOREAN TRIPLES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 95 / Issue 1 / February 2017
- Published online by Cambridge University Press:
- 26 September 2016, pp. 5-13
- Print publication:
- February 2017
-
- Article
-
- You have access
- Export citation
RAMANUJAN CAYLEY GRAPHS OF FROBENIUS GROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 94 / Issue 3 / December 2016
- Published online by Cambridge University Press:
- 26 September 2016, pp. 373-383
- Print publication:
- December 2016
-
- Article
-
- You have access
- Export citation
FORMS OF DIFFERING DEGREES OVER NUMBER FIELDS
- Part of
-
- Journal:
- Mathematika / Volume 63 / Issue 1 / 2017
- Published online by Cambridge University Press:
- 26 September 2016, pp. 92-123
- Print publication:
- 2017
-
- Article
- Export citation
On the Bateman–Horn conjecture for polynomials over large finite fields
- Part of
-
- Journal:
- Compositio Mathematica / Volume 152 / Issue 12 / December 2016
- Published online by Cambridge University Press:
- 21 September 2016, pp. 2525-2544
- Print publication:
- December 2016
-
- Article
- Export citation
On Goren–Oort stratification for quaternionic Shimura varieties
- Part of
-
- Journal:
- Compositio Mathematica / Volume 152 / Issue 10 / October 2016
- Published online by Cambridge University Press:
- 21 September 2016, pp. 2134-2220
- Print publication:
- October 2016
-
- Article
- Export citation
Modular embeddings of Teichmüller curves
- Part of
-
- Journal:
- Compositio Mathematica / Volume 152 / Issue 11 / November 2016
- Published online by Cambridge University Press:
- 21 September 2016, pp. 2269-2349
- Print publication:
- November 2016
-
- Article
- Export citation
PARTIAL INDEFINITE THETA IDENTITIES
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 102 / Issue 2 / April 2017
- Published online by Cambridge University Press:
- 19 September 2016, pp. 255-289
- Print publication:
- April 2017
-
- Article
-
- You have access
- Export citation
ON POINTS WITH POSITIVE DENSITY OF THE DIGIT SEQUENCE IN INFINITE ITERATED FUNCTION SYSTEMS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 102 / Issue 3 / June 2017
- Published online by Cambridge University Press:
- 09 September 2016, pp. 435-443
- Print publication:
- June 2017
-
- Article
-
- You have access
- Export citation
ON THE AUTOMORPHISMS OF THE NONSPLIT CARTAN MODULAR CURVES OF PRIME LEVEL
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 224 / Issue 1 / December 2016
- Published online by Cambridge University Press:
- 09 September 2016, pp. 74-92
- Print publication:
- December 2016
-
- Article
-
- You have access
- HTML
- Export citation
On the Chromatic Number of Random Cayley Graphs
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 26 / Issue 2 / March 2017
- Published online by Cambridge University Press:
- 09 September 2016, pp. 248-266
-
- Article
- Export citation
Effective Hasse principle for the intersection of two quadrics
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 19 / Issue A / 2016
- Published online by Cambridge University Press:
- 26 August 2016, pp. 73-82
-
- Article
-
- You have access
- Export citation
Databases of elliptic curves ordered by height and distributions of Selmer groups and ranks
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 19 / Issue A / 2016
- Published online by Cambridge University Press:
- 26 August 2016, pp. 351-370
-
- Article
-
- You have access
- Export citation
Explicit isogenies in quadratic time in any characteristic
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 19 / Issue A / 2016
- Published online by Cambridge University Press:
- 26 August 2016, pp. 267-282
-
- Article
-
- You have access
- Export citation