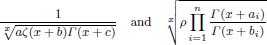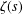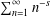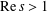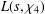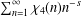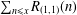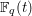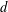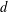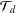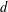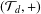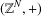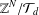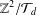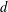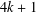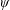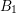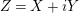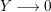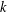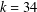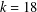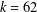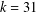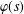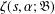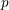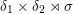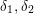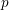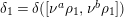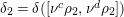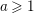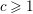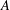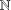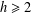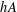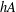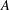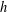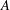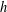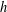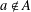Refine listing
Actions for selected content:
2818 results in 11xxx
SPECTRAL ZETA FUNCTIONS FOR THE QUANTUM RABI MODELS
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 229 / March 2018
- Published online by Cambridge University Press:
- 01 December 2016, pp. 52-98
- Print publication:
- March 2018
-
- Article
-
- You have access
- HTML
- Export citation
WEIGHT CHANGING OPERATORS FOR AUTOMORPHIC FORMS ON GRASSMANNIANS AND DIFFERENTIAL PROPERTIES OF CERTAIN THETA LIFTS
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 228 / December 2017
- Published online by Cambridge University Press:
- 28 November 2016, pp. 186-221
- Print publication:
- December 2017
-
- Article
-
- You have access
- HTML
- Export citation
ELLIPTIC K3 SURFACES ASSOCIATED WITH THE PRODUCT OF TWO ELLIPTIC CURVES: MORDELL–WEIL LATTICES AND THEIR FIELDS OF DEFINITION
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 228 / December 2017
- Published online by Cambridge University Press:
- 09 November 2016, pp. 124-185
- Print publication:
- December 2017
-
- Article
-
- You have access
- HTML
- Export citation
The Monotonicity and Log-Behaviour of Some Functions Related to the Euler Gamma Function
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 60 / Issue 2 / May 2017
- Published online by Cambridge University Press:
- 09 November 2016, pp. 527-543
-
- Article
- Export citation
ON A NEW CIRCLE PROBLEM
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 103 / Issue 2 / October 2017
- Published online by Cambridge University Press:
- 08 November 2016, pp. 231-249
- Print publication:
- October 2017
-
- Article
-
- You have access
- Export citation
Affine Weyl group multiple Dirichlet series: type
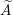 $\widetilde{A}$
$\widetilde{A}$
- Part of
-
- Journal:
- Compositio Mathematica / Volume 152 / Issue 12 / December 2016
- Published online by Cambridge University Press:
- 08 November 2016, pp. 2503-2523
- Print publication:
- December 2016
-
- Article
- Export citation
ON POLY-EULER NUMBERS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 103 / Issue 1 / August 2017
- Published online by Cambridge University Press:
- 03 November 2016, pp. 126-144
- Print publication:
- August 2017
-
- Article
-
- You have access
- Export citation
ALGEBRAIC AND GEOMETRIC PROPERTIES OF LATTICE WALKS WITH STEPS OF EQUAL LENGTH
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 95 / Issue 2 / April 2017
- Published online by Cambridge University Press:
- 02 November 2016, pp. 338-346
- Print publication:
- April 2017
-
- Article
-
- You have access
- Export citation
INTRINSIC DIOPHANTINE APPROXIMATION ON GENERAL POLYNOMIAL SURFACES
- Part of
-
- Journal:
- Mathematika / Volume 63 / Issue 1 / 2017
- Published online by Cambridge University Press:
- 02 November 2016, pp. 250-259
- Print publication:
- 2017
-
- Article
- Export citation
A New Quasi-Monte Carlo Technique Based on Nonnegative Least Squares and Approximate Fekete Points
- Part of
-
- Journal:
- Numerical Mathematics: Theory, Methods and Applications / Volume 9 / Issue 4 / November 2016
- Published online by Cambridge University Press:
- 17 November 2016, pp. 640-663
- Print publication:
- November 2016
-
- Article
- Export citation
THE HOLOMORPHY CONJECTURE FOR NONDEGENERATE SURFACE SINGULARITIES
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 227 / September 2017
- Published online by Cambridge University Press:
- 28 October 2016, pp. 160-188
- Print publication:
- September 2017
-
- Article
-
- You have access
- HTML
- Export citation
ON THE FOURIER COEFFICIENTS OF SIEGEL MODULAR FORMS
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 234 / June 2019
- Published online by Cambridge University Press:
- 21 October 2016, pp. 1-16
- Print publication:
- June 2019
-
- Article
-
- You have access
- HTML
- Export citation
ON A PROBLEM OF ERDÖS AND MAHLER CONCERNING CONTINUED FRACTIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 95 / Issue 2 / April 2017
- Published online by Cambridge University Press:
- 19 October 2016, pp. 183-186
- Print publication:
- April 2017
-
- Article
-
- You have access
- Export citation
ON PAIRS OF GOLDBACH–LINNIK EQUATIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 95 / Issue 2 / April 2017
- Published online by Cambridge University Press:
- 19 October 2016, pp. 199-208
- Print publication:
- April 2017
-
- Article
-
- You have access
- Export citation
REMARKS ON THE MIXED JOINT UNIVERSALITY FOR A CLASS OF ZETA FUNCTIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 95 / Issue 2 / April 2017
- Published online by Cambridge University Press:
- 19 October 2016, pp. 187-198
- Print publication:
- April 2017
-
- Article
-
- You have access
- Export citation
STABLE MODELS OF LUBIN–TATE CURVES WITH LEVEL THREE
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 225 / March 2017
- Published online by Cambridge University Press:
- 18 October 2016, pp. 100-151
- Print publication:
- March 2017
-
- Article
-
- You have access
- HTML
- Export citation
COMPOSITION FACTORS OF A CLASS OF INDUCED REPRESENTATIONS OF CLASSICAL
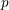 $p$ -ADIC GROUPS
$p$ -ADIC GROUPS
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 227 / September 2017
- Published online by Cambridge University Press:
- 18 October 2016, pp. 16-48
- Print publication:
- September 2017
-
- Article
-
- You have access
- HTML
- Export citation
A NOTE ON ASYMPTOTIC NONBASES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 95 / Issue 1 / February 2017
- Published online by Cambridge University Press:
- 13 October 2016, pp. 1-4
- Print publication:
- February 2017
-
- Article
-
- You have access
- Export citation
DYNAMICS ON SUPERSINGULAR K3 SURFACES AND AUTOMORPHISMS OF SALEM DEGREE 22
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 227 / September 2017
- Published online by Cambridge University Press:
- 13 October 2016, pp. 1-15
- Print publication:
- September 2017
-
- Article
-
- You have access
- HTML
- Export citation
2-ADIC INTEGRAL CANONICAL MODELS
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 4 / 2016
- Published online by Cambridge University Press:
- 05 October 2016, e28
-
- Article
-
- You have access
- Open access
- Export citation
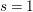
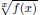 is given, which is a continuous analogue of a result of Wang and Zhu. On the other hand, the log-behaviour of the functions
is given, which is a continuous analogue of a result of Wang and Zhu. On the other hand, the log-behaviour of the functions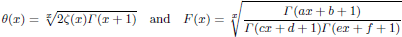
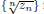 for some combinatorial sequences (including the Bernoulli numbers, the tangent numbers, the Catalan numbers, the Fuss–Catalan numbers, and the binomial coefficients
for some combinatorial sequences (including the Bernoulli numbers, the tangent numbers, the Catalan numbers, the Fuss–Catalan numbers, and the binomial coefficients 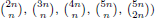 are demonstrated. In particular, this contains some results of Chen
are demonstrated. In particular, this contains some results of Chen 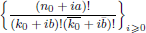
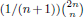 and the central binomial coefficients
and the central binomial coefficients 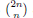 are infinitely log-monotonic, and strengthens one result of Su and Wang that
are infinitely log-monotonic, and strengthens one result of Su and Wang that 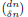 is log-convex in
is log-convex in